Сказка про точку прямую луч и отрезок

Тема: «Точка. Кривая линия. Прямая линия. Отрезок. Луч».

Возраст обучающихся: подготовительная группа

Форма организации занятия: занятие-путешествие

Тип занятия: изучение нового материала и первичное закрепление знаний.

Цель занятия:

создать условия по формированию представлений о точке, линии, прямой, отрезке, луче; уметь находить на чертеже геометрические фигуры

Задачи:

Образовательные:

сформировать первичные представления о точке, линии, прямой, отрезке, луче; о их сходстве и различии;
совершенствовать умения выполнять простейшие геометрические построения;

Развивающие:

развивать умение грамотно называть луч, прямую, отрезок;
развивать творческое математическое мышление посредством введения эвристических вопросов; воображения,
развивать речь, коммуникативные качества;

Воспитательные — воспитывать познавательный интерес к математике.

Интеграции ОО: «Познавательное развитие», «Социально-Коммуникативное развитие», «Речевое развитие».

Методы организации занятия:

Словесные методы обучения (беседа
Методы практической работы.
Метод игры (игра-путешествие)
Наглядный метод обучения (иллюстрация, демонстрация)
Метод проблемного обучения (постановка проблемных вопросов, создание проблемных ситуаций)
Метод наблюдения.

Оборудование: магнитная доска, магниты.

Демонстрационный материал:

Карточки с изображением незнакомого дошкольникам геометрического материала.
Иллюстрации основных геометрических фигур

Раздаточный материал:

Картинки с задачами
Детские билеты на ракету

«Волшебные» карандаши (по количеству детей).
Карточки «Соедини точки» — с геометрическими фигурами (по количеству детей).

1 этап — организационный

Результат деятельности этапа: определение уровня внимания, активности, восприятия, настроя детей на предстоящее занятие.

Здравствуйте, ребята! Посмотрите, что у меня в руках. Да, это глобус- модель нашей Земли. На нашей планете очень много стран и городов. Чтобы их увидеть мы путешествуем по нашей земле. А как мы можем добраться до других городов, на чем? (полететь на самолете, поплыть на пароходе, на лодке, поехать на поезде, машине, можно даже на велосипеде)

Сегодня мы отправимся в небольшое путешествие в волшебную страну под названием Геометрия. В эту необычную страну можно попасть с помощью необычных билетов, их дают только тем, кто разгадает небольшие задачки (работа по карточкам).

Билеты получены, можно отправляться в путь.

Физминутка

Один, два, три, четыре, пять (ходьба на месте)

В космос мы летим опять (соединить руки над головой)

Отрываюсь от земли (подпрыгнуть)

Долетаю до луны (руки в стороны, покружиться)

На орбите повисим (покачать руками вперед-назад)

На планету мы спешим (ходьба на месте)

2 этап — изучение нового учебного материала

Результат деятельности этапа: осознанное усвоение обучающимися нового учебного материала и первичное закрепление новых знаний

Итак мы прибыли в страну Геометрия. Посмотрите на ее жителей (показываю, рассматриваем геометрические фигуры, назовите их; спрашиваю знакомы ли с объёмными геометрическими фигурами, попробуйте назвать их).

Здесь живет самый маленький житель – Точка. Это геометрическая фигура. (Работа на доске. На доске начерчены точка, кривая линия, прямая линия, отрезок, луч).

Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (Линии на доске).

-Какие это линии? (Ответы детей).

-Прямые линии, ребята, похожи на натянутые веревочки, а веревочки, которые не натянули – это кривые линии. Сколько прямых на доске? (2). Сколько кривых? (2).

-Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца. Я бесконечная!» (Показываю изображение прямой на доске).

-Очень интересно стало точке посмотреть. Сама-то точка малюсенькая. Вышла она и не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч (Показываю изображение луча).

Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало. Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч. И на месте луча появился отрезок. У него уже были начало и конец (Показываю изображение отрезка).

-Понравилась сказка? (Ответы детей). Что узнали о прямой линии? (Она бесконечная) Покажите ее на доске.

-Что узнали о луче? (У него есть начало, но нет конца) Покажите ее на доске

-Что узнали об отрезке? (У него есть начало и конец). Покажите ее на доске

Практическая работа по карточкам

-Давайте посмотрим. Сколько здесь точек?

-Какое задание мы можем сделать с этим множеством точек?

-Правильно, проведите по точкам линии, чтобы получить картинку.

-Давайте посмотрим, что у вас получилось.

-Что вы видите на карточках? (квадраты)

— Сколько их? (3)

-С помощью чего мы получили форму геометрических фигур?

-Одинаковы ли они по размерам? (нет)

—Разукрасьте самый большой квадрат синим цветом, самый маленький желтым цветом, средний по размеру – красным.

-Какого цвета квадрат слева от красного, какой – справа.

-Ребята, как Вы думаете, как можно определите длину прямых сторон? (Ответы детей).

-Что значит определить «на глаз»? (Не измеряя). Есть разные мерки, какие вы помните? (пядь, локоть, сажень)

Для того, чтобы не было путаницы, люди придумали общую мерку – сантиметр. С помощью чего мы можем измерить стороны нашего квадрата? (линейки). Давайте измерим длину квадрата. Что вы заметили? (все стороны равны)

3 этап – итоговый

Результат деятельности этапа: самооценка обучающимися собственной деятельности; определение перспектив развития творческой деятельности в данной образовательной области.

Итак, мы встретились с уже знакомыми жителями страны Геометрии. И познакомились с новыми.

-С чем мы сегодня познакомились?

-Что такое точка? (геометрическая фигура, покажи)

-Что такое линия? (нет ни начала, ни конца, покажи)

— Что такое луч? (есть начало, нет конца, покажи)

— Что такое отрезок? (есть начало и конец, покажи)

-Наше путешествие подошло к концу. Пора отправляться обратно в путь!

Один, два, три, четыре, пять (ходьба на месте)

В космос мы летим опять (соединить руки над головой)

Отрываюсь от земли (подпрыгнуть)

Долетаю до луны (руки в стороны, покружиться)

На орбите повисим (покачать руками вперед-назад)

И опять домой спешим (ходьба на месте)

Скажем до свидания, до новых встреч в стране Геометрия.

Вот мы снова в нашем детском саду в своей группе.

Понравилось ли вам наше путешествие?

В какое путешествие хотели бы отправится еще раз?

А теперь мы попрощаемся с нашими гостями.

Источник

Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и подсказками к решению (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6.

Геометрия 7. Контрольные работы
Геометрия 7. Самостоятельные работы

Геометрия 7 класс. Урок 21.
Самостоятельная работа № 6 (задания)

Основная дидактическая цель урока: совершенствовать навыки решения задач на применение второго признака равенства треугольников. Перед решением задач необходимо повторить конспекты: «Треугольник. Равенство треугольников», «ЗАДАЧИ на Признаки равенства треугольников».

I уровень сложности (легкий)

Вариант 1 (уровень 1)

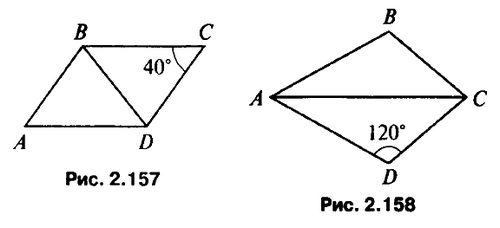
Дано: АВ = СD, ВС = DA, ∠C = 40° (рис. 2.157).
Доказать: ΔABD = ΔCDB. Найти: ∠A.
На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника. Докажите, что MD = ND.
В треугольниках АВС и А₁В₁С₁ АВ = А₁В₁, ∠A = ∠A₁, ∠B = ∠B₁. Точки D и D₁ лежат соответственно на сторонах АС и А₁С₁, причем CD = C₁D₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните отрезки BD и B₁D₁.

Вариант 2 (уровень 1)

Дано: AD = АВ, CD = CB, D= 120° (рис. 2.158).
Доказать: ΔDAC = ΔBAC. Найти: ∠B.
На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – высота треугольника. Докажите, что MD = ND.
В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, АС = A₁C₁, ∠A = ∠A₁. Точки D и D₁ лежат соответственно на сторонах АС и A₁C₁, ∠DBC = ∠D₁B₁C₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните углы ВDC и B₁C₁D₁.

II уровень сложности (средний)

Вариант 1 (уровень 2)

Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.
В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, ∠А = ∠A₁, ∠B = ∠B₁. На сторонах ВС и В₁С₁ отмечены точки D и D₁ так, что ∠CAD = ∠C₁A₁D₁. Докажите, что: а) ΔADC = ΔA₁D₁C₁; б) ΔADB = ΔA₁D₁B₁.

Вариант 2 (уровень 2)

Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.
В треугольниках DEC и D₁E₁C₁ DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁. На сторонах DE и D₁E₁ отмечены точки P и P₁ так, что ∠DCP = ∠D₁C₁P₁. Докажите, что: a) ΔDCP = ΔD₁C₁P₁; б) ΔCPE = ΔC₁P₁E₁.

III уровень сложности (сложный)

Вариант 1 (уровень 3)

Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).
В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Вариант 2 (уровень 3)

Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).
В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Самостоятельная работа № 6
Указания к решению и ОТВЕТЫ

С-6. I уровень сложности (ответы)

Докажите самостоятельно.

Геометрия 7 Атанасян Самостоятельная 6

С-6. II уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 2)

№ 1. Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
Докажите самостоятельно.

№ 2. На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и медиана BD является его биссектрисой (рис. 2.160).
2) ΔMBN – равнобедренный с основанием MN, так как МВ = BN (МВ = ВА– МА; BN = ВС – МС, ВА = ВС, МА = NC). BD – биссектриса ΔMBN, и по свойству биссектрисы равнобедренного треугольника она является медианой, т. е. ВО – медиана ΔMBN.

№ 3. В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, ∠А = ∠A₁, ∠B = ∠B₁. На сторонах ВС и В₁С₁ отмечены точки D и D₁ так, что ∠CAD = ∠C₁A₁D₁.
Докажите, что: а) ΔADC = ΔA₁D₁C₁; б) ΔADB = ΔA₁D₁B₁.

Доказательство:
а) ΔАВС = ΔА₁В₁С₁ по стороне и прилежащим к ней углам (АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁ по условию задачи) (рис. 2.161). ΔADC = ΔA₁D₁C₁ по стороне и прилежащим к ней углам (АС = А₁С₁, ∠C = ∠C₁ из равенства треугольников АВС и А₁В₁С₁, ∠CAD = ∠C₁A₁D₁ по условию задачи).
б) Так как ΔADC = ΔA₁D₁C₁, то DC = D₁C₁, следовательно, равны отрезки BD и B₁D₁ (ВС = В₁С₁ из равенства треугольников АВС и А₁В₁С₁). Так как АВ = А₁В₁, ∠B = ∠B₁ из равенства треугольников АВС и А₁В₁С₁ и BD = В₁D₁, то ΔABD = ΔA₁B₁D₁ по двум сторонам и углу между ними.

Задания и Ответы на Вариант 2 (уровень 2)

№ 1. Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Докажите самостоятельно.

№ 2. Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и высота BD, проведенная из его вершины к основанию, является и его биссектрисой, т. е. ВО – биссектриса ∠ABC и ∠MBN тоже (рис. 2.163).
2) ΔMBN – равнобедренный с основанием MN (ВМ = ВА + AM, BN = ВС + CN; так как ВА = ВС и АМ = CN, то ВМ = BN). В равнобедренном ΔMBN биссектриса ВО, проведенная из его вершины к основанию, является и его высотой.

№ 3. В треугольниках DEC и D₁E₁C₁ DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁. На сторонах DE и D₁E₁ отмечены точки P и P₁ так, что ∠DCP = ∠D₁C₁P₁. Докажите, что: a) ΔDCP = ΔD₁C₁P₁; б) ΔCPE = ΔC₁P₁E₁.

Доказательство:
а) ΔDEC = ΔD₁E₁C₁ по стороне и прилежащим к ней углам (DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁) (рис. 2.164).
Так как ΔDEC = ΔD₁E₁C₁, то DC = D₁C₁. Тогда ΔDCP= ΔD₁C₁P₁ по стороне и прилежащим к ней углам (DC = D₁C₁, ∠D = ∠D₁, ∠PCD= ∠P₁C₁D₁).
б) Так как ΔDEC = ΔD₁E₁C₁, тo EC = E₁C₁, ∠ECD = ∠E₁C₁D₁.
Так как ∠ECD = ∠E₁C₁D₁, ∠PCD = ∠P₁C₁D₁, a ∠ECP = ∠ECD – ∠DCP, ∠E₁C₁P₁ = ∠E₁C₁D₁ – ∠D₁C₁P₁, ∠ECP = ∠E₁C₁P₁.
Так как ЕС = E₁C₁ ∠E = ∠E₁, ∠ECP = ∠E₁C₁P₁, то ΔPEC = ΔP₁E₁C₁ по стороне и прилежащим к ней углам.

Геометрия 7 Атанасян Самостоятельная 6.

С-6. III уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).

Доказательство: ΔМЕК = ΔPFK по двум сторонам и углу между ними (ME = FP, МК = КР по условию задачи, ∠M = ∠P как углы при основании равнобедренного ΔMNP). Следовательно, КЕ= KF.
ΔKEN = ΔKFN по трем сторонам (КЕ = KF; KN – общая сторона; NE = NF, так как NE = MN – ME, NF = PN – PF, a MN = PN, ME = PF). Следовательно, ∠EKN = ∠FKN.
Так как ∠EKN = ∠FKN, то KN – биссектриса угла ∠EKF.

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания равнобедренного ΔАВС с основанием АС, то BD – медиана, а значит, и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.167).
∠NBA = ∠CBM как вертикальные.
∠NBD = ∠NBA + ∠ABD, a ∠MBD = ∠MBC + ∠CBD. Так как ∠ABD = ∠CBD, ∠MBC = ∠NBA, то ∠NBD = ∠MBD.
ΔNBD = ΔMBD по двум сторонам и углу между ними (NB = МВ; BD – общая сторона; ∠NBD = ∠MBD).

Задания и Ответы на Вариант 2 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).

Доказательство: ΔМЕК = ΔPFK по стороне и прилежащим к ней углам (МК = КР, так как К – середина МР; ∠MKE = ∠PKF по условию задачи; ∠M = ∠P как углы при основании равнобедренного ΔMNP).
Так как ΔМЕК = ΔPFK, то ME = PF, следовательно, EN = FN (EN = MN – ME, FN = PN – PF, a MN = FN как боковые стороны равнобедренного треугольника).
Так как ΔМЕК = ΔPFK, то КЕ = KF. ΔNEK = ΔNFK по трем сторонам (NK – общая сторона, NE = EF, ЕК = ЕК).

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания АС равнобедренного ΔАВС, то BD – медиана и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.170).
∠NBA = ∠CBM как вертикальные. Поэтому ∠NBD = ∠MBD (∠NBD = ∠NBA + ∠ABD, ∠MBD = ∠MBC + ∠CBD, a ∠NBA = ∠CBM, ∠ABD = ∠CBD).
ΔBDM = ΔBDN по стороне и прилежащим к ней углам (BD – общая сторона, ∠NBD = ∠MBD, ∠BDM = ∠BDN).

Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Геометрия 7. Поурочные планы
Геометрия 7. Самостоятельные работы

Источник

Фрагмент технологической карты урока по математике на тему: «Точка. Прямая линия. Кривая линия. Отрезок. Луч.»

Преподаватель: Карасева Л.П.

Ейск, 2021 г.

Тема урока: «Точка. Прямая линия. Кривая линия. Отрезок. Луч»

Цель: формирование представлений у учащихся о начальных геометрических понятий «точка», «кривая линия», « прямая», «отрезок». Подготовить к пониманию необходимости специальных приёмов действий для проведения прямой линии. Учить распознавать их.

Личностные УУД: 1)выражать свое мнение, точку зрения; 2)проявлять положительное отношение к уроку, 3) понимать необходимость в учении; 4)проявлять самостоятельность в различных видах деятельности.

Познавательные УУД: 1) ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; 2)добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; 3)анализировать, сравнивать, сопоставлять, обобщать факты.

Регулятивные УУД: 1) определять и формулировать цель и задачи на уроке; 2) умение осуществлять самоанализ своей деятельности; 3)вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; 4)высказывать своё предположение.

Коммуникативные УУД: 1) сотрудничать со сверстниками; 2) оказывать взаимопомощь сверстникам; 3) оформлять свои мысли в устной форме; 4) слушать и понимать речь других; 5) совместно договариваться о правилах поведения и следовать им; 6) совершенствовать работу в группах, парах, классом.

№ п/п

Этап урока

Деятельность учителя

Деятельность учащегося

Формируемые УУД

Актуализация фиксирование индивидуальных затруднений в пробном действии

Отступаем одну клетку вниз от числа.

-Ребята, я вам бужу читать задание, ваша задача решить его и ответ записать к себе в тетрадь. Числа записываем в строчку, через запятую, пропуская одну клетку.

Найдите сумму чисел 3 и 4. ( 7)
Уменьшите 10 на 2. ( 8 )
Увеличьте 4 на 2. ( 6 )
1 слагаемое — 5, 2 слагаемое – такое же. Чему равна сумма? ( 10 )
10 без 1. ( 9 )

Давайте проверим с вами данную работу.

Устный счёт

-Ребята, посмотрите на слайд. Кто это такой? В какой сказке мы познакомились с этим персонажем?

Катится колобок и тренируется в счете. И мы с вами сейчас потренируемся и проведем устный счет.

1) хором посчитаем от 1 до 10

2) от 8 до 2

3) сколько пальцев на 2-х руках?

4) сколько лап у одной собаки?

5) какое число при счете идет девятым?

6) какое число на 1 больше, числа 5?

7) какое число является предыдущим для числа 3?

сколько хвостов у восьми кошек?

9) 1 слагаемое – 5, 2 слагаемое – 2, чему равна сумма этих чисел?

10) в одной коробке 5 карандашей, а другой – ни одного. Сколько всего карандашей в двух коробках?

(Во время выполнения задания контролирую работу учащихся.)

(При выполнении задания в случаи неверных ответов задаю наводящие)

-Молодцы! Не допустили ни одной ошибки

Прекрасно работают на уроке ….

Учащиеся записывают числа в строчку, через запятую.

Отвечают хором на вопросы устного счета

Личностные УУД (1)

Познавательные УУД (1)

Регулятивные УУД(1)

Выявление места и причины затруднения

-Итак, сейчас мы с вами отправимся в путешествие на волшебном паровозе, но путешествие не легкое, на нашем пути будут появляться трудности, но мы с ними справимся!

Посмотрите на доску. Что на ней изображено?

Все ли они одинаковые?

Назовите и покажите те геометрические фигуры, которые вам знакомы.

Для того чтобы их изобразить, что рисовали?

О чем же будем говорить на уроке?)

Это и будет темой нашего урока.

Фигуры и линии

Нет

Квадрат, круг, треугольник

Линии и точки

о линиях и точках

Личностные УУД (1)

Познавательные УУД (1)

Регулятивные УУД(1)

Построение проекта выхода из затруднения

— У каждого из вас, на парте есть карандаш и листочек бумаги. Возьмите карандаш и поставьте его на лист.

А теперь поднимите карандаш, что у нас осталось на листе?

Этот след и есть точка – геометрическая фигура.

В стране Геометрии жила-была точка. Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям. Посмотрите, какие это были линии.

-На что похожи прямые линии?

-Сколько прямых линий?

— На что похожи кривые линии?

— Сколько кривых?

Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!

-Очень интересно сталь точке посмотреть на неё. Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На её месте появился луч.

-Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.

-Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила опять на луч.

-И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.

-Вот так маленькая точка смогла изменить жизнь больших линий.

-Ребята, какие же геометрические фигуры живут в стране геометрии?

Учащиеся слушают мини сказку о геометрических фигурах.

Прямые и кривые

Похожи на натянутые верёвочки

Которые не натянуты

Точка, прямая линия, кривая линия, луч, отрезок.

Личностные УУД (1)

Познавательные УУД (1,3)

Регулятивные УУД (3,4)

КоммуникативныеУУД(3,4)

Реализация построенного проекта выхода из затруднения

— Откройте учебник. Посмотрите на рисунок на стр.40 . Расскажите, чем прямая линия отличается от кривой.

-Что вы запомнили о прямой линии, луче, отрезке?

— Как начертить прямую линию?

— Как начертить отрезок?

— Прочитайте задание на полях на стр.40. Как узнать, какой отрезок самый длинный.

— Посчитайте и скажите, какой отрезок самый длинный.

— Какой отрезок самый короткий?

Учащиеся работают с учебником.

Прямая линия натянута, кривая-нет.

Провести по линейке линию

Поставить две точки и соединить их

Посчитать клетки линии

Синий

Красный

Личностные УУД (3)

Познавательные УУД(1)

Регулятивные УУД(2,3,4)

Коммуникативные УУД(3,4,5)

Первичное закрепление с проговариванием во внешне речи

— Рассмотрите рисунок на стр.41.

Найдите и покажите на рисунке кривые линии, отрезки, лучи.

Физминутка

Математику люблю.

Спину ровно я держу.

Вправо, влево наклоняюсь,

Как прямая, выправляюсь.

Руки в стороны раздвину,

Вверх ладошки подниму

И отрезок покажу.

Раз присядем, два присядем

И на место тихо сядем.

Давайте вместе с вами начертим отрезок, проверяйте свой чертеж по-моему, который на доске.

Теперь начертим луч, прямую линию, кривую линию и начертим точку.

Учащиеся работают по рисунку на странице 41.

Учащиеся выполняют упражнения физминутку за учителем

Чертят в тетради все изученные раннее фигуры.

Личностные УУД (3)

Познавательные УУД(1)

Регулятивные УУД(2,3,4)

Коммуникативные УУД(3,4)

Самостоятельная работа с самопроверкой по принятому эталону

Итак, ребята вам необходимо будет выполнить самостоятельную работу.

Вам необходимо разделить линии на группы. Это прямые линии и кривые. В первых квадратах вам необходимо написать номера прямых линий, а во-вторых квадратах номера кривых линий.

Учащиеся подписывают карточки и выполняют самостоятельную работу.

Личностные УУД (3)

Познавательные УУД(1)

Регулятивные УУД(2,3,4)

Коммуникативные УУД(3,4)

Источник

Введение

На мой взгляд, рейкастинг — великолепная концепция, понять которую не так сложно, но качественных ресурсов по ней очень мало. Я расскажу о математике, лежащей в её основе, чтобы вы при желании с лёгкостью могли реализовать её в своих будущих проектах. Постараюсь сделать объяснение как можно более понятным, рассказать о всех тонкостях и проблемах, с которыми вы можете столкнуться. Также мы поговорим об оптимизации и о том, как сильно вам могут помочь пространственные хэш-карты. Ещё я напишу простые интерактивные примеры, с которыми вы сможете поэкспериментировать. Учтите, что демо написаны максимально простым образом, не ожидайте увидеть в них код уровня энтерпрайза — мы изучаем саму концепцию, а не реализацию.

Что такое рейкастинг?

«Рейкастинг (ray casting, „испускание лучей“) — самый простой из множества алгоритмов рендеринга компьютерной графики, использующих геометрический алгоритм трассировки лучей (ray tracing). Алгоритмы рендеринга на основе трассировки лучей работают на уровне изображений, выполняя рендеринг трёхмерных сцен в двухмерные изображения…

Принцип рейкастинга заключается в том, чтобы попиксельно отслеживать испускаемые из глаза лучи, чтобы найти ближайший объект, препятствующий пути каждого луча — представьте, что изображение — это проволочная сетка, а каждый квадрат сетки — это пиксель. Таким образом мы можем определить объект, который видит глаз через этот пиксель.» — Википедия

Ну, звучит не очень понятно, правда? Давайте упростим объяснение. Рейкастинг — это популярная фундаментальная техника, используемая для определения видимости определённых объектов (полигонов) трассировкой лучей из глаза (например, персонажа игрока) до каждого пикселя (ну, в нашем случае это не совсем так, но подробнее об этом позже) и нахождением самых ближайших пересечений с объектами.

Где может использоваться рейкастинг?

Рейкастинг можно использовать по-разному, особенно в трёхмерном пространстве. Я выделю три наиболее важных по моему мнению применения, часто встречающихся в игровых 2D-движках:

Создание 3D-перспективы на 2D-карте

Самой известной игрой, использующей эту технику, является Wolfenstein 3D. Лучи в ней трассировались для определения ближайших объектов, а их расстояние от позиции игрока использовалось для правильного масштабирования.

Простой рейкастинг с коррекцией фишай Лукаса Виейра

Задача точки в многоугольнике

Задача PIP (point-in-polygon) заключается в определении того, находится ли точка внутри, снаружи или на границе многоугольника. При помощи алгоритма рейкастинга мы можем посчитать, сколько раз точка пересекает края многоугольника. Если количество пересечений чётно, то точка находится снаружи многоугольника. Если количество пересечений нечётно, то точка находится внутри или на границе многоугольника.

b2fbb4fdf939bd74c176f0d1ee9b9969

Решение задачи точки в многоугольнике при помощи рейкастинга

Видимость объектов и испускание света

В статье мы рассмотрим именно эту задачу — определение видимости объектов для игрока и освещение видимой области.

7051874fcaf08c725e5f3b74095da460

Видимость объектов и испускание света

Видимость объектов и испускание света в 2D-играх

В этом разделе мы рассмотрим такие базовые понятия, как точки пересечения, испускание лучей, сортировка точек пересечения для освещения видимой области, а также несколько слов скажем о кругах. На каждом из этапов я буду писать интерактивные демо, чтобы вы не запутались и могли сразу же увидеть результаты.

Точка пересечения отрезка и луча

Здесь мы поговорим о точках пересечения. Давайте поэтапно разберёмся, как их находить и использовать. Сначала мы выведем параметрическое уравнение прямой, вычислим точки пересечения, а затем узнаем, как эффективно определять ближайшую из них.

Вывод параметрического уравнения прямой

Давайте сначала поговорим о прямых и их параметрическом уравнении.

f35f77fbd2caa312cdff87bed99b8dc3

Пример прямой линии

Мы можем выразить вектор $inline$ следующим уравнением: $inline$ , где $inline$ — параметр уравнения, определяющий, насколько мы растягиваем $inline$ или сжимаем $inline$ , и меняем ли мы направление $inline$ вектора $inline$ относительно вектора $inline$ .

Позвольте продемонстрировать пару примеров:

f7141166d1efa7fc4e25cfe65a18172c

Пример параметров параметрического уравнения прямой

Как вы могли заметить, мы можем использовать $inline$ как коэффициент масштабирования: $inline$ . Мы воспользуемся этим при определении ближайшей точки пересечения.

Теперь мы можем легко увидеть, нужно ли нам, чтобы точка находилась на:

Выяснив всё это, мы наконец можем вывести параметрическое уравнение:

$display$

Если вы всё ещё не понимаете, что здесь происходит, то рекомендую вам прочитать потрясающую короткую лекцию Норма Прокупа: Parametrizing a Line Segment — Concept.

Вычисление точки пересечения

Допустим, точка $inline$ является точкой пересечения отрезка прямой, заданного точками $inline$ и $inline$ , и луча, заданного точками $inline$ и $inline$ . Тогда точку $inline$ можно выразить как систему из двух уравнений:

$display$

Вычислим $inline$ и $inline$ :

$begin{align} s(B_x - A_x) + A_x &= r(D_x - C_x) + C_x Rightarrow s = tfrac{r(D_x - C_x) + (C_x - A_x)}{B_x - A_x} s(B_y - A_y) + A_y &= r(D_y - C_y) + C_y Rightarrow r = tfrac{s(B_y - A_y) + (A_y - C_y)}{D_y - C_y} end{align}$

.
Подставим $inline$ во второе уравнение:

$begin{align} &tfrac{r(D_x - C_x) + (C_x - A_x)}{B_x - A_x} (B_y - A_y) + A_y = r(D_y - C_y) + C_y [10pt] &r tfrac{(D_x - C_x)(B_y - A_y)}{B_x - A_x} + tfrac{(C_x - A_x)(B_y - A_y)}{B_x - A_x} + A_y = r(D_y - C_y) + C_y [10pt] &r (tfrac{(D_x - C_x)(B_y - A_y)}{B_x - A_x} - (D_y - C_y)) = (C_y - A_y) - tfrac{(C_x - A_x)(B_y - A_y)}{B_x - A_x} [10pt] &r tfrac{(D_x - C_x)(B_y - A_y) - (D_y - C_y)(B_x - A_x)}{B_x - A_x} = tfrac{(C_y - A_y)(B_x - A_x) - (C_x - A_x)(B_y - A_y)}{B_x - A_x} [10pt] &r = tfrac{(C_y - A_y)(B_x - A_x) - (C_x - A_x)(B_y - A_y)}{(D_x - C_x)(B_y - A_y) - (D_y - C_y)(B_x - A_x)} [10pt] &r = tfrac{(B_x - A_x)(C_y - A_y) - (C_x - A_x)(B_y - A_y)}{(D_x - C_x)(B_y - A_y) - (B_x - A_x)(D_y - C_y)} [10pt] end{align}$

Подставим $inline$ в первое уравнение:

$begin{align} &s(B_x - A_x) + A_x = tfrac{s(B_y - A_y) + (A_y - C_y)}{D_y - C_y} (D_x - C_x) + C_x [10pt] &s(B_x - A_x) + A_x = s tfrac{(B_y - A_y)(D_x - C_x)}{D_y - C_y} + tfrac{(A_y - C_y)(D_x - C_x)}{D_y - C_y} + C_x [10pt] &s (tfrac{(B_y - A_y)(D_x - C_x)}{D_y - C_y} - (B_x - A_x)) = (A_x - C_x) - tfrac{(A_y - C_y)(D_x - C_x)}{D_y - C_y} [10pt] &s tfrac{(B_y - A_y)(D_x - C_x) - (B_x - A_x)(D_y - C_y)}{D_y - C_y} = tfrac{(A_x - C_x)(D_y - C_y) - (A_y - C_y)(D_x - C_x)}{D_y - C_y} [10pt] &s = tfrac{(A_x - C_x)(D_y - C_y) - (A_y - C_y)(D_x - C_x)}{(B_y - A_y)(D_x - C_x) - (B_x - A_x)(D_y - C_y)} [10pt] &s = tfrac{(A_x - C_x)(D_y - C_y) - (D_x - C_x)(A_y - C_y)}{(D_x - C_x)(B_y - A_y) - (B_x - A_x)(D_y - C_y)} [10pt] end{align}$

Вычислив $inline$ и $inline$ , мы можем вычислить $inline$ при помощи одного из уравнений системы.

o484mbmsntsghda1mdyp ckj9c8

Демо 1 — все точки пересечения

[Прим. пер.: в оригинале статьи все демо интерактивны.]

Поиск ближайшей точки пересечения

Для правильной отрисовки видимой области нам нужна только ближайшая точка пересечения. Наивным решением было бы вычисление расстояний между точкой начала луча и точками пересечения при помощи теоремы Пифагора: $sqrt{(C_x - P_x) ^ 2 + (C_y - P_y) ^ 2}$ . Но вы помните о параметре уравнения прямой? Я уже говорил, что мы можем использовать его как коэффициент масштабирования. Так как мы хотим сравнить расстояния на луче, то можем найти наименьшее значение параметра $inline$ : $|overrightarrow{CP_1}| < |overrightarrow{CP_2}| Leftrightarrow |r_1| < |r_2|$ .

1utzua6cflv4jzt7pzqu1j98uao

Демо 2 — ближайшая точка пересечения

Испускание лучей

В этом разделе мы рассмотрим два способа испускания лучей. Мы сравним их и расскажем об их достоинствах и недостатках.

Испускание лучей по углу смещения

Первый способ — это испускание лучей во всех направлениях с заданным углом смещения. Например, мы можем испустить 30 лучей, смещённых на $inline$ . Давайте сначала узнаем, как сгенерировать все эти лучи.

Пусть $inline$ будет начальной точкой всех лучей, а $inline$ — некой точкой на прямой, проходящей через $inline$ под углом $inline$ :

85e4cde20b74870710c6907e764b4e66

Линия из заданной точки под неким углом

Мы можем задать $inline$ как $inline$ , а $inline$ как $inline$ (наша ось Y перевёрнута, отсюда и минус).

Теперь нам нужно вывести формулы для $inline$ и $inline$ :

$left{begin{align} sin(phi) &= tfrac{dy}{mathit{dist}} Rightarrow dy = mathit{dist} * sin(phi) cos(phi) &= tfrac{dx}{mathit{dist}} Rightarrow dx = mathit{dist} * cos(phi) end{align}right.$

В нашем случае $inline$ — это произвольное значение больше нуля (мы ищем любую точку на прямой), поэтому для упрощения вычислений вполне можно допустить, что $inline$ . С учётом всего этого $inline$ , где $inline$ — это угловое смещение.

zbu3znsnelwslfplbn 1jghncjy

Демо 3 — испускание лучей на угол смещения

Испускание лучей в вершины

Вероятнее всего, вам больше подойдёт испускание лучей в вершины. Вместо испускания лучей во всех направлениях мы просто можем испускать их в вершины многоугольников. Если количество вершин невелико, мы можем сэкономить вычислительные ресурсы, не испуская бесполезные лучи. В следующих разделах мы увидим, как это влияет на плавность анимаций, а также узнаем, как оптимизировать весь процесс.

Демо 4 — испускание лучей в вершины

Освещение видимой области

Сейчас начинается самое интересное. Мы осветим видимую область заливкой огромного многоугольника.

Сортировка точек пересечения

Чтобы создать правильный порядок вершин для построения многоугольника, нужно сначала отсортировать их по углу. Для этого мы используем функцию $inline$ . Подробнее о ней можно прочитать здесь.

Давайте сравним оба способа испускания лучей:

Демо 5 — испускание лучей с углами смещения (заполненная видимая область)

Демо 6 — испускание лучей в вершины (заполненная видимая область)

Оба способа выглядят ошибочными, скачущими и неточными. Давайте разберёмся, почему.

Испускание лучей с небольшим смещением

Заметьте, что происходит, когда лучи испускаются непосредственно на вершины — они должны идти дальше этой вершины, но мы получаем только ближайшую точку пересечения:

696e28e7cf11f74e0e91ecd38f2968db

Проблема лучей на вершинах

Самым популярным решением является испускание двух дополнительных лучей со смещением на небольшой угол (в обоих направлениях) для каждого испущенного луча. Рассмотрим луч $inline$ , начинающийся в $inline$ и проходящий через $inline$ . Нам нужна такая точка $inline$ , чтобы луч $inline$ был повёрнут на $inline$ с начальной точкой $inline$ . $inline$ будет иметь следующие координаты:

${begin{align} C_x &= (B_x - A_x)cos(phi) - (B_y - A_y)sin(phi) + A_x C_y &= (B_y - A_y)cos(phi) + (B_x - A_x)sin(phi) + A_y end{align}$

Обратите внимание, что для первого способа это делать не нужно — мы просто прибавляем или вычитаем смещение из угла, который вычисляем. Дополнительные объяснения можно прочитать в этой статье.

6c3590ffc1737002922b082cd8032b67

Проблема лучей в вершинах решена

Давайте посмотрим, как ведёт себя освещение после этих изменений:

cldaykcxy76enx khlv9scppui

Демо 7 — испускание лучей с углом смещения (заполненная видимая область с дополнительными лучами)

n8qqlzdh ifbbu00i3k6hkvuu80

Демо 8 — испускание лучей в вершины (заполненная видимая область с дополнительными лучами)

В случае первого способа это не особо улучшило ситуацию. Мы можем уменьшить смещение углов (увеличив количество лучей), но результат всё равно будет плохим. С другой стороны, второй способ выглядит очень плавным и точным. Далее мы больше не будем говорить о первом способе.

Круг видимости и фонарик

Иногда нам бывает нужно ограничивать видимость для игрока. Этого можно достичь, создав область усечения нужной формы. В показанных ниже демо я использовал метод CanvasRenderingContext2D.clip().

Демо 9 — круг видимости

Демо 10 — фонарик

Как вы могли заметить, это не является оптимизацией — мы всё равно вычисляем все точки пересечения. Мы вернёмся к этому после того, как узнаем о пространственных хэш-картах.

А как насчёт окружностей?

Я редко видел случаи испускания лучей на окружности. Считайте этот раздел дополнением, в котором я вкратце о них упомяну. Я покажу уравнения и простые демо, а дальнейшую работу оставлю вам.

Точка пересечения окружности и луча

Пусть $inline$ будет точкой пересечения, $inline$ — начальной точкой луча, $inline$ — точкой на луче, $inline$ — точкой центра окружности, а $inline$ — её радиусом.

$left{begin{align} P_x &= t(B_x - A_x) + A_x P_y &= t(B_y - A_y) + A_y r ^ 2 &= (P_x - C_x) ^ 2 + (P_y - C_y) ^ 2 end{align}right.$

Решаем относительно $inline$ :

$begin{align} r ^ 2 &= P_x ^ 2 - 2P_xC_x + C_x ^ 2 + P_y ^ 2 - 2P_yC_y + C_y ^ 2 r ^ 2 &= (t(B_x - A_x) + A_x) ^ 2 - 2(t(B_x - A_x) + A_x)C_x + C_x ^ 2 &+ (t(B_y - A_y) + A_y) ^ 2 - 2(t(B_y - A_y) + A_y)C_y + C_y ^ 2 r ^ 2 &= t ^ 2 (B_x - A_x) ^ 2 + 2t(B_x - A_x)A_x + A_x ^ 2 - 2t(B_x - A_x)C_x - 2A_xC_x + C_x ^ 2 &+ t ^ 2 (B_y - A_y) ^ 2 + 2t(B_y - A_y)A_y + A_y ^ 2 - 2t(B_y - A_y)C_y - 2A_yC_y + C_y ^ 2 0 &= t ^ 2 ((B_x - A_x) ^ 2 + (B_y - A_y) ^ 2) &+ 2t((B_x - A_x)A_x - (B_x - A_x)C_x + (B_y - A_y)A_y - (B_y - A_y)C_y) &+ A_x ^ 2 - 2A_xC_x + C_x ^ 2 + A_y ^ 2 - 2A_yC_y + C_y ^ 2 - r ^ 2 0 &= t ^ 2 ((B_x - A_x) ^ 2 + (B_y - A_y) ^ 2) &+ 2t((B_x - A_x)(A_x - C_x) + (B_y - A_y)(A_y - C_y)) &+ (A_x - C_x) ^ 2 + (A_y - C_y) ^ 2 - r ^ 2 end{align}$

Решаем квадратное уравнение:

$left{begin{align} a &= (B_x - A_x) ^ 2 + (B_y - A_y) ^ 2 b &= 2((B_x - A_x)(A_x - C_x) + (B_y - A_y)(A_y - C_y)) c &= (A_x - C_x) ^ 2 + (A_y - C_y) ^ 2 - r ^ 2 Delta &= b ^ 2 - 4ac end{align}right.$

Только в случае $inline$ :

$begin{align} t = tfrac{-b}{2a} end{align}$

Только в случае $inline$ :

$left{begin{align} P_x &= t(B_x - A_x) + A_x P_y &= t(B_y - A_y) + A_y end{align}right.$

Только в случае $inline$ :

$left{begin{align} t_1 &= tfrac{-b -sqrt{Delta}}{2a} t_2 &= tfrac{-b +sqrt{Delta}}{2a} end{align}right.$

Только в случае $inline$ :

$left{begin{align} P_{i_x} &= t_i(B_x - A_x) + A_x P_{i_y} &= t_i(B_y - A_y) + A_y end{align}right.$

rffmpe2piewypncu9tcwvfohcbe

Демо 11 — пересечение луча и окружности

Испускание лучей на окружности

Нам нужно найти две касательные к заданной окружности, проходящие через точку начала луча.

Пусть $inline$ — точки касательных, $inline$ — точка начала луча, $inline$ — центр окружности, а $inline$ — её радиус. Также мы будем перемещать все точки при помощи вектора переноса $overrightarrow{v} = (-C_x, -C_y)$ : $X^prime = X + overrightarrow{v}$ так, чтобы центр окружности находился в $inline$ .

Из уравнения окружности:

$P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = r ^ 2$

Из линии перпендикуляра к радиусу окружности:

$left{begin{align} & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = r ^ 2 & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = P_x ^ prime A_x ^ prime + P_y ^ prime A_y ^ prime end{align}right.$

Решаем систему уравнений:

$left{begin{align} & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = r ^ 2 & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = P_x ^ prime A_x ^ prime + P_y ^ prime A_y ^ prime end{align}right.$

$begin{align} & r ^ 2 = P_x ^ prime A_x ^ prime + P_y ^ prime A_y ^ prime & P_x ^ prime = tfrac{r ^ 2 - P_y ^ prime A_y ^ prime }{A_x ^ prime} text{, where } A_x ^ prime neq 0 end{align}$

Подставляем $inline$ в первое уравнение:

$begin{align} & (tfrac{r ^ 2 - P_y ^ prime A_y ^ prime }{A_x ^ prime}) ^ 2 + P_y ^ {prime ^ 2} = r ^ 2 & tfrac{r ^ 4 - 2 r ^ 2 P_y ^ prime A_y ^ prime + (P_y ^ prime A_y ^ prime) ^ 2}{A_x ^{prime ^ 2}} + P_y ^ {prime ^ 2} = r ^ 2 & r ^ 4 - 2 r ^ 2 P_y ^ prime A_y ^ prime + (P_y ^ prime A_y ^ prime) ^ 2 + P_y ^ {prime ^ 2} A_x ^{prime ^ 2} = r ^ 2 A_x ^{prime ^ 2} & P_y ^ {prime ^ 2} (A_x ^{prime ^ 2} + A_y ^{prime ^ 2}) - P_y ^ prime 2r ^ 2 A_y ^ prime + r ^ 4 - r ^ 2 A_x ^ {prime ^ 2} = 0 end{align}$

Решаем квадратное уравнение:

$left{begin{align} a &= A_x ^{prime ^ 2} + A_y ^{prime ^ 2} b &= - 2r ^ 2 A_y ^ prime c &= r ^ 4 - r ^ 2 A_x ^ {prime ^ 2} Delta &= b ^ 2 - 4ac end{align}right.$

Только в случае $inline$ :

$left{begin{align} P_y ^ prime &= tfrac{-b}{2a} P_x ^ prime &= tfrac{r ^ 2 - P_y ^ prime A_y ^ prime }{A_x ^ prime} end{align}right.$

$left{begin{align} P_x &= P_x ^ prime + C_x P_y &= P_y ^ prime + C_y end{align}right.$

Только в случае $inline$ :

$left{begin{align} P_{1_y} ^ prime &= tfrac{-b -sqrt{Delta}}{2a} P_{2_y} ^ prime &= tfrac{-b +sqrt{Delta}}{2a} P_{i_x} ^ prime &= tfrac{r ^ 2 - P_{i_y} ^ prime A_y ^ prime }{A_x ^ prime} end{align}right.$

$left{begin{align} P_{i_x} &= P_{i_x} ^ prime + C_x P_{i_y} &= P_{i_y} ^ prime + C_y end{align}right.$

Но есть ещё одна проблема — это не сработает, если $inline$ . Присмотримся к следующему уравнению: $inline$ . Если $inline$ , уравнение принимает следующий вид: $inline$ — больше мы не можем подставить $inline$ . Вот как решить эту систему уравнений, если такое случится:

Решаем систему уравнений:

$left{begin{align} & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = r ^ 2 & P_x ^ {prime ^ 2} + P_y ^ {prime ^ 2} = P_x ^ prime A_x ^ prime + P_y ^ prime A_y ^ prime & A_x ^ prime = 0 end{align}right.$

$begin{align} & r ^ 2 = P_y ^ prime A_y ^ prime & P_y ^ prime = tfrac{r ^ 2}{A_y ^ prime} text{, where } A_y ^ prime neq 0 end{align}$

Подставим $inline$ в первое уравнение:

$begin{align} & P_x ^ {prime ^ 2} + (tfrac{r ^ 2}{A_y ^ prime}) ^ 2 = r ^ 2 & P_x ^ {prime ^ 2} + tfrac{r ^ 4}{A_y ^ {prime ^ 2}} = r ^ 2 & P_x ^ {prime ^ 2} A_y ^ {prime ^ 2} + r ^ 4 = r ^ 2 A_y ^ {prime ^ 2} & P_x ^ {prime ^ 2} A_y ^ {prime ^ 2} + r ^ 4 - r ^ 2 A_y ^ {prime ^ 2} = 0 end{align}$

Решим квадратное уравнение:

$left{begin{align} a &= A_y ^ {prime ^ 2} b &= 0 c &= r ^ 4 - r ^ 2 A_y ^ {prime ^ 2} Delta &= b ^ 2 - 4ac end{align}right.$

Только в случае $inline$ :

$left{begin{align} P_x ^ prime &= tfrac{-b}{2a} P_y ^ prime &= tfrac{r ^ 2}{A_y ^ prime} end{align}right.$

$left{begin{align} P_x &= P_x ^ prime + C_x P_y &= P_y ^ prime + C_y end{align}right.$

Только в случае $inline$ :

$left{begin{align} P_{1_x} ^ prime &= tfrac{-b -sqrt{Delta}}{2a} P_{2_x} ^ prime &= tfrac{-b +sqrt{Delta}}{2a} P_{i_y} ^ prime &= tfrac{r ^ 2}{A_y ^ prime} end{align}right.$

$left{begin{align} P_{i_x} &= P_{i_x} ^ prime + C_x P_{i_y} &= P_{i_y} ^ prime + C_y end{align}right.$

Заметьте, что тоже самое мы можем сделать при $inline$ , однако это необязательно. Если $inline$ , то решений нет.

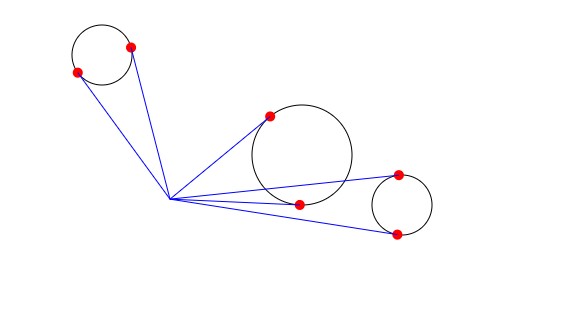
Демо 12 — испускание лучей на окружности

Способы оптимизации

В этом разделе мы поговорим об использовании пространственных хэш-карт и модифицированного алгоритма рисования линий Брезенхэма. Я не буду вдаваться в подробности реализации, потому что они широко доступны в Интернете. Однако я напишу несколько демо, чтобы вы могли их тестировать и придумывать новые идеи их применения.

Пространственные хэш-карты

Пока мы отрисовываем все многоугольники и вычисляем все точки пересечения, но это практически бесполезно. В большинстве случаев игровая область гораздо больше окна обзора. При помощи пространственных хэш-карт мы можем быстро определять, какие многоугольники видны игроку и выполнять адекватные вычисления.

По сути, мы хотим разделить игровую область на меньшие ячейки (заданного размера). Каждая ячейка состоит из списка, содержащего фигуры (чаще всего это отрезки прямых). Если одна фигура растянулась на несколько ячеек, то она будет включена во все эти ячейки.

Из названия этой методики понятно, что в ней используются хэш-карты (т.е. ячейки будут иметь названия вида X+»:»+Y), но в нашем случае желательней будет простой 2D-массив.

Вот простое демо, показывающее, как это может работать:

d9afrq2osklbfs lbdkoeotb3as

Демо 13 — пространственные хэш-карты

Как говорилось выше, мы можем применять их для окон обзора, а также для окружностей видимости и фонариков.

Линия сверхпокрытия на основе алгоритма Брезенхэма

При помощи пространственных хэш-карт и модифицированного алгоритма отрисовки линий Брезенхэма мы можем эффективным образом обходить сетку, выполняя минимальное количество проверок. Алгоритм должен завершать выполнение после обнаружения первой ячейки с точкой пересечения.

Подробнее об алгоритме отрисовки линий Брезенхэма можно прочитать здесь, а об его модифицированной версии — здесь.

cvcwmw6zogo7jknyruerfvzodj0

Демо 14 — Линия сверхпокрытия на основе алгоритма Брезенхэма

Всё имеет свой конец

Простите, к сожалению, я говорю об этой статье, а не о лучах.

Думаю, мы раскрыли всё необходимое для того, чтобы вы могли приступить к работе. Если я найду что-то, требующее дальнейшего объяснения, то постараюсь дополнить статью. Кроме того, я создал небольшую шпаргалку для напоминания о некоторых темах и выведенных формулах.

Если вам понравилась статья, то поставьте звёздочку и подпишитесь на этот репозиторий на GitHub.

Источник

Инфоурок › Алгебра ›Презентации›Сравнение и измерение отрезков. Геометрия 7 класс учебник Атанасян

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Начальные геометрические сведения 7 класс геометрия Уроки № 3-4 Сравнение и измерение отрезков

2 слайд Описание слайда:

Цели: Ввести понятие равенства геометрических фигур. Научить сравнивать отрезки. Ввести понятие длины отрезка. Рассмотреть свойства длин отрезков. Различные единицы длины измерения отрезков. Решение задач на нахождение длины.

3 слайд Описание слайда:

Вспомним! Две геометрические фигуры называются равными, если при наложении они совмещаются.

4 слайд Описание слайда:

Если концы отрезков совпадают то отрезки АВ и СD равны. АВ = СD А В C D

5 слайд Описание слайда:

Если концы отрезков не совпадают то отрезки АВ и СD не равны. АВ AB C D А В

6 слайд Описание слайда:

Если С – середина отрезка MN MC = СN MN = 2MC = 2NC

7 слайд Описание слайда:

Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. MN = MC + CN

8 слайд Описание слайда:

Длину отрезка АВ называют расстоянием между точками А и В 13.07.2012 www.konspekturoka.ru А B IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

9 слайд Описание слайда:

А В ОЕ = 1 см АВ = 5 см Длину АВ измеряют расстоянием между точками А и В с помощью единичного отрезка ОЕ – единичный отрезок О

10 слайд Описание слайда:

10 см =1 дм 1см = 10 мм 100 см = 1 м 1км = 1000м Русские меры длины. Среди русских мер длины древнейшими являются локоть и сажень. Первое упоминание сажени встречается в летописи XI века. Для измерения длины кроме сантиметра применяют и другие единицы длины

11 слайд Описание слайда:

Аршин – мера, возникшая при торговле с народами Востока. Название единицы происходит от персидского слова «арш», что значит локоть. Сажень – единица длины равная 3 аршинам. Кроме сажени, на Руси употреблялась косая сажень (2,48 м) и маховая (1,76 м).

12 слайд Описание слайда:

Отметьте в тетради точки К и М. С помощью линейки постройте отрезок КМ. Отметьте на этом отрезке точки Р и Т. Назовите отрезки, на которые эти точки делят отрезок КМ. На какие отрезки точка Т делит отрезок КМ? KP, PT, TM, KT, PM.

TM, KT.

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 К М Р Т №31

13 слайд Описание слайда:

А, В, С  а, АВ = 12 см, ВС = 13,5 см АС — ? Решение Возможны случаи: а) точка В лежит между А и С, тогда АС = АВ + ВС, АС = 12 + 13,5 = 25,5 (см). б) точка А лежит между В и С, тогда АС = СВ — АВ, АС = 13,5 — 12 = 1,5 (см). Ответ: 25,5 см или 1,5 см. Дано: Найти: 12 см 13,5 см 12 см 13,5 см

14 слайд Описание слайда:

В  АС, АВ = 3,7 см, АС = 7,2 см ВС — ? Решение ? Так как В  АС, АВ + ВС = АС, ВС = АС — АВ ВС = 7,2 – 3,7 = 3,5 (см). Ответ: BС = 3,5см. Дано: Найти: 3,7 см 7,2 см №31

15 слайд Описание слайда:

АВ = 64 см, С – середина АВ, D — лежит на луче СА, СD = 15 см. ВD, DA — ? Решение АВ = 64 см, С – середина АВ, тогда АС = СВ = 32 см. СD = 15 см, DA = AC – DC = 32 – 15 = 17 (см) ВD = DC + CB = 15 + 32 = 47 (см) Ответ: BD = 47см, DA = 17 см. Дано: Найти: №34

16 слайд Описание слайда:

AF = FB, BK = KC, AC = 5 см. FK — ? Решение 2FB + 2BK = 5 см, FB + BK = 2,5 см, FB +BK = FK, Поэтому FK = 2,5 см. Ответ: FK = 2,5см. По условию AF = FB, BK = KC, тогда AF + FB + BK +KC = AC, Дано: Найти: C F

17 слайд Описание слайда:

О, А, В – лежат на одной прямой, ОА = 12 см, ОВ = 9 см. расстояние между серединами отрезков ОА и ОВ — ? Решение Пусть М – середина отрезка ОА, N – середина отрезка ОВ.

Возможны два случая: а) если точка О лежит на отрезке АВ, то МО = АО : 2 = 6 см, NO = BO : 2 = 4,5 см.

Расстояние между серединами отрезков ОА и ОВ равно длине отрезка MN, a MN = MO + NO = 6 + 4,5 = 10,5 (см) Дано: Найти: В М

18 слайд Описание слайда:

б) если точка О не лежит на отрезке АВ б) если точка О не лежит на отрезке АВ, то МО = АО : 2 = 6 см, NO = BO : 2 = 4,5 см. Пусть по условию: М – середина отрезка ОА, N – середина отрезка ОВ. Решение MN = MO – ON = 6 – 4,5 = 1,5 (см). Ответ: а) 10,5 см; б) 1,5 см. A N

19 слайд Описание слайда:

Ответить на вопросы: Какие геометрические фигуры называются равными? Какие отрезки равны? Чему равна длина отрезка? Как измерить длину отрезка? Какие есть единицы измерения длин?

Общая информация

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Источник: https://infourok.ru/sravnenie-i-izmerenie-otrezkov-geometriya-klass-uchebnik-atanasyan-666778.html

Длины отрезков: как сравнить и найти середину или концы единичного отрезка координатной прямой, правила об этом и примеры на рисунке

Сравнить 2 отрезка на плоскости — это типичная задача по геометрии для учеников 7 класса. Существует несколько разных методов выполнения данного сравнения, и мы подробно расскажем о каждом из них.

Подобного рода задачи выполняются элементарно и являются основой для изучения дальнейшего материала. Стоит один раз запомнить этот несложный процесс, и в дальнейшем уже не возникнет никаких трудностей с аналогичными заданиями.

Метод наложения

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения.
Измерение длин.

Пусть нам даны два отрезка AB и СD:

Совместим начало отрезка AB и СD (точки A и С).

MK = KV, K — середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок STтак, чтобы он совпал с отрезком HG.
В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.
Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ (т.к. 3 , QL = PO (т.к. 5 = 5).

Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
Если при измерении отрезков их длины равны, то отрезки равны.

Источник:

Как сравнить 2 отрезка: способы решения задачи

Что такое отрезок

Прежде чем рассказать, как сравнить 2 отрезка, давайте разберем, что такое отрезок на плоскости.

Список профессий связанных с физикой

Определение из учебника по геометрии гласит, что отрезок — это часть прямой, которая с двух сторон ограничивается двумя точками.

Если рассматривать одну прямую, отрезком будет считаться множество, которое состоит из двух разных точек этой прямой (собственно, концов отрезка), а также остального множества из всех точек, которые располагаются между ними (так называемых внутренних точек).

Сравнение двух отрезков

Итак, в вопросе о том, как сравнить 2 отрезка, можно выделить следующие методы:

Наложение. Для того чтобы выполнить сравнение двух отрезков, нужно выполнить наложение одного из них на другой. Соответственно, тот отрезок, который будет содержать внутри себя второй отрезок целиком, больше. Если концы этих отрезков совпали — значит, их длины равны.
Второй способ, как сравнить 2 отрезка в геометрии — это выяснить, на какое количество единиц отличается их длина. Для этого нужно при помощи линейки с одинаковыми значениями провести измерение сначала одного отрезка, затем другого, и из первого результата вычесть второй.

В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.

Вывод

Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.

Источник:

Прямая и отрезок, измерение и сравнение отрезков

Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.

Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины.

Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.

Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках.

С какой скоростью Земля вращается вокруг Солнца?

Понятия прямой и точки связаны тремя аксиомами геометрии:

Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.

Для двух прямых актуально их взаимное расположение. Возможны три случая:

Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.

В этой статье мы не будем подробно останавливаться на этих понятиях.

Отрезок

Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками. Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.

Отрезки будем обозначать двумя её точками концов в квадратных скобках.

Сравнение отрезков

Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.

Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.

Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:

Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу.
Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.

Источник:

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Как найти разность чисел в математике?

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.
Это интересно: как разложить на множители квадратный трехчлен?
Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

визуальный способ;
измерительный;
сравнение наложением;
сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> или √ 73, значит, Da > Db.
Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Источник:

Источник: https://obraz-ola.ru/tehnicheskie-nauki/kak-sravnit-dliny-otrezkov.html

Геометрия 7 класс.Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Запомните!

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

На рисунке изображена прямая a и точки D, F, G и H. Точки F и G лежат на прямой a. Точки D и H не лежат на прямой a.

В тексте точку обозначают символом «(·)». Принадлежность и непринадлежность точки прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как зеркальное отображение буквы «Э» или как знак евро «€» .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

(·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
(·)G ∈ a — точка G принадлежит прямой a;
(·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
(·)H ∉ a — точка H не принадлежит прямой a.

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Прямая a
Прямая f
Прямая CH
Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE, прямая EF и прямая DF — это три разных имени одной и той же прямой.

Проведите прямую, обозначьте её буквой a и отметьте точки A и B, лежащие на этой прямой, и точки P, Q и R, не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a, используя символы ∈ и ∉.

Решение задачи

Проведём прямую.

Обозначим её буквой a.

Отметим точки (·)A и (·)B, лежащие на прямой a.

Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.

Опишем взаимное расположение точек и прямой.

(·)A ∈ a
(·)B ∈ a
(·)P ∉ a
(·)Q ∉ a
(·)R ∉ a

Задача решена.

На рисунке прямые a и b не пересекаются. Прямые b и c пересекаются.

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с).

В тексте пересечение прямых обозначают символом ∩. Информацию на рисунке выше можно записать следующим образом:

b ∩ c — прямые b и с пересекаются;
a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M. Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями пересечение прямых в точке записывается так: e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Запомните!

Через любые две точки можно провести прямую, и притом только одну.

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Запомните!

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M.

Третий случай расположения прямых

Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B.

Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно.

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Теперь прямая a пересекается с прямой b, прямая b пересекается с прямой c и прямая c пересекается с прямой a.

В этом случае у нас только одна точка пересечения всех прямых — точка (·)D.

Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D. Тогда получится три точки пересечения — (·)D, (·)E и (·)F.

Прямая a пересекается с прямой b в точке (·)D, прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E. Условие задачи выполнено.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Запомните!

Отрезок — часть прямой, ограниченная двумя точками.

Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T.

Сам отрезок можно назвать ST или TS. Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник: http://math-prosto.ru/?page=pages/point_straight_segment/point_straight_segment_geometry_7_grade.php

Отрезок

Длина отрезка
Равные отрезки
Сравнение отрезков
Середина отрезка

Отрезок – это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка – это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок – это отрезок, длина которого принимается за единицу. Следовательно, длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

AB = 6 см.

Свойства длин отрезков:

Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Длины равных отрезков равны.

Равные отрезки

Равные отрезки – это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка – это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

CA CA.

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB

Источник: https://izamorfix.ru/matematika/planimetriya/otrezok.html

Видеоурок «Сравнение отрезков и углов. Измерение отрезков»

Содержание:

§ 1 Равенство геометрических фигур

В повседневной жизни мы нередко встречаемся с равными фигурами: два одинаковых листа бумаги, две облицовочные плитки, две одинаковые тарелки. Представим, что вы решили украсить свой походный костюм нашивкой.

Для этого вы рисуете на бумаге изображение, вырезаете его, затем накладываете на материал, из которого будет нашивка, и вновь вырезаете по границе. Фигуры, вырезанные из бумаги и из материала, равны, потому что они совмещаются одна с другой.

На равенстве совмещенных фигур основаны раскрой материала для шитья одежды на фабриках, штамповка плоских деталей на заводе и т.д.

Итак, две геометрические фигуры называются равными, если их можно совместить наложением.

§ 2 Сравнение отрезков и углов

Рассмотрим два отрезка АВ и СD и ответим на вопрос: равны они или нет?

Для этого наложим отрезок АВ на отрезок СD так, чтобы один конец отрезков АВ совпал с концом отрезка СD, т.е. точка А совпала с точкой С.

Если при этом два других конца совместятся, т.е. точка В совпадет с точкой D, то отрезки АВ и СDравны.

Если точка В не совпадет с точкой D, то меньшим отрезком считается тот отрезок, который составляет часть другого. На рисунке отрезок СD составляет часть отрезка АВ, поэтому отрезок СD меньше отрезка АВ. Пишут СD

А теперь возьмем отрезок МN и отметим на нем точку О так, что отрезки МО и NО будут равны.

Такая точка О, которая делит отрезок пополам, т.е. на два равных отрезка, называется серединой отрезка.

Рассмотрим два неразвернутых угла АОВ и СОD.

Чтобы сравнить два неразвернутых угла, надо наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон.

Если сторона ОА совместится со стороной ОС, а сторона ОВ совместится со стороной ОD, то углы АОВ и СОD равны. Если же сторона ОВ не совместится со стороной ОD, то меньшим считается тот угол, который составляет часть другого.

На рисунке угол АОВ меньше угла СОD, так как угол АОВ составляет часть угла СОD.

Рассмотрим развернутый угол, т.е. угол, обе стороны которого лежат на одной прямой. Неразвернутый угол составляет часть развернутого угла, поэтому любой развернутый угол больше любого неразвернутого угла, а два развернутых угла всегда равны.

А теперь из вершины угла проведем луч так, что он будет делить этот угол на два равных угла, такой луч называется биссектрисой угла.

На рисунке луч ОС – биссектриса угла АОВ, так как этот луч исходит из вершины угла АОВ и делит этот угол на два равных угла АОС и СОВ.

§ 3 Измерение отрезков. Единицы измерения

Фигуры на практике не всегда можно совместить наложением, например, невозможно таким образом проверить, равны ли земельные участки. Поэтому приходится искать другие способы установления равенства фигур. Для сравнения, например, отрезков пользуются измерением, т.е. находят длины отрезков.

Чтобы измерить отрезок, надо его сравнить с некоторым другим отрезком, принятым за единицу измерения. Такой отрезок называют еще масштабным отрезком. За единицу измерения можно взять отрезок длиной 1 мм, 1 см, 1 дм, 1м, 1 км или другой отрезок. Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.

Это число показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.

Равные отрезки имеют равные длины.
Меньший отрезок имеет меньшую длину.
Когда произвольная точка С делит отрезок АВ на два отрезка, то длина всего отрезка АВ равна сумме длин отрезков АС и СВ.
Длину отрезка называют также расстояниеммежду его концами.

Международной единицей измерения выбран метр, это отрезок, приближенно равный одной сорока миллионной части земного меридиана. Эталон метра хранится во Франции, а копии хранятся во всех странах, в том числе и в России.

Для измерения очень больших расстояний, например, измерение расстояний между планетами солнечной системы, используют единицу измерения световой год, это путь, который свет проходит в течение одного года.

В старину на Руси использовались другие единицы измерения аршин, локоть, сажень.

Для измерения расстояний пользуются различными инструментами, например, линейка, штангенциркуль, рулетка.

§ 4 Решение задачи по теме урока

Решим задачу.

Отрезок ОD длиной 28 см разделен точкой М на два отрезка. Найдите расстояние между серединами получившихся отрезков ОМ и МD.

Решение:

Расстояние между серединами отрезков ОМ и МD– это расстояние между точками А и В, оно равно сумме отрезков АМ и МВ.

Точка А – середина отрезка ОМ, значит отрезки ОА и АМ равны, точка В – середина отрезка МD, значит отрезки МВ и ВD равны. Отрезок ОD равен сумме отрезков ОА, АМ, МВ, ВD. Так как отрезок ОА равен отрезку АМ, отрезок МВ равен ВD, то длина отрезка ОD равна удвоенной сумме отрезков АМ и МВ, т.е. двум отрезкам АВ.

Следовательно, длину отрезка АВ находим так: 28:2=14 см. Это искомое расстояние между серединами отрезков ОМ и МD.

Список использованной литературы:

Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М. : Просвещение, 2013. – 383 с.: ил.
Гаврилова Н.Ф. Поурочные разработки по геометрии 7 класс. — М.: «ВАКО», 2004, 288с. – (В помощь школьному учителю).
Белицкая О.В. Геометрия. 7 класс. Ч.1. Тесты. – Саратов: Лицей, 2014. – 64 с.

Использованные изображения:

Источник: https://znaika.ru/catalog/7-klass/geometry/Sravnenie-otrezkov-i-uglov.-Izmerenie-otrezkov.html

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

…

Вконтакте
Facebook
Twitter
Google+
Мой мир

Оглавление:

Способы сравнения двух отрезков
Измерение длины
Наложение друг на друга
Сравнение в координатной сетке
Примеры

Способы сравнения двух отрезков

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

визуальный способ;
измерительный;
сравнение наложением;
сравнение в координатной сетке.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> или √ 73, значит, Da > Db.
Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.
Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБПри помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8>2, значит, CD>AB, то есть отрезок CD длиннее AB.

Источник: https://obrazovanie.guru/nauka/matematika/kak-sravnit-dva-otrezka-sposoby-i-primery.html

Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

A B C

1 2 3

Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

a b c

Линия может быть

замкнутой, если её начало и конец находятся в одной точке,
разомкнутой, если её начало и конец не соединены

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.

Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

самопересекающейся
без самопересечений

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

B A

Прямые могут быть

пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
параллельными, если не пересекаются, не имеют общей точки.

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

Точка разделяет прямую на две части — два луча

A A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

B A

Лучи совпадают, если

расположены на одной и той же прямой,
начинаются в одной точке,
направлены в одну сторону

C B A

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

B A

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.

✂ B A ✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

B A

Задача: где прямая, луч, отрезок, кривая?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

A B C D E 64 62 127 52

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

A B C D E F 120 60 58 122 98 141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.

Источник: http://shpargalkablog.ru/2015/11/point-line-straight-ray-segment.html

Урок 3 Получить доступ за 50 баллов Отрезок. Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.
Длина в геометрии — это величина, которая характеризует протяженность.
Длина отрезка — это расстояние между концами отрезка.
Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.
Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

2. Совмещение отрезков — более точный способ сравнения отрезков.

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.
По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.
Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.
Значит, отрезок ОЕ короче отрезка АВ.
Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.
В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.
Пример:
Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.
Соединим ножки циркуля с концами С и D отрезка СD.
Приложим циркуль с заданным раствором к отрезку АЕ.
Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).
Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.
Большим будет являться тот отрезок, длина которого больше.
Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.
Отрезки (звенья) ломаной линии называют сторонами многоугольника.
Общие точки двух отрезков (сторон) многоугольника называют его вершинами.
Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.
Количество сторон и количество углов в многоугольнике совпадают.
Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.
Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.
Рассмотрим пример:
На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.
Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.
Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.
Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.
Периметр многоугольника — это сумма длин всех сторон.
Периметр многоугольника принято обозначать заглавной латинской буквой Р
Найдем периметр многоугольника АBCDEF (изображенного на рисунке):
РАВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.
Существует огромное множество различных видов многоугольников.
Обычно многоугольники различают по числу сторон и углов.
Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник — 6 углов и 6 сторон.
Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.
Треугольник — плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.
Рассмотрим пример:

На рисунке изображен треугольник АBC (Δ АBC).
А, В, С — вершины треугольника АBC.
Отрезки AB, BC, АC— стороны треугольника АBC.
Периметр треугольника- это сумма длин трех его сторон.
Найдем периметр треугольника АBC (изображенного на рисунке):
РАВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Источник: https://ladle.ru/education/matematika/5class/otrezok-dlina

Источник

Геометрия 7 класс. Урок 21.Самостоятельная работа № 6 (задания)

I уровень сложности (легкий)

III уровень сложности (сложный)

Самостоятельная работа № 6Указания к решению и ОТВЕТЫ

С-6. I уровень сложности (ответы)

С-6. II уровень сложности (ответы)

С-6. III уровень сложности (ответы)

Введение

Что такое рейкастинг?

Где может использоваться рейкастинг?

Создание 3D-перспективы на 2D-карте

Задача точки в многоугольнике

Видимость объектов и испускание света

Видимость объектов и испускание света в 2D-играх

Точка пересечения отрезка и луча

Вывод параметрического уравнения прямой

Вычисление точки пересечения

Поиск ближайшей точки пересечения

Испускание лучей

Испускание лучей по углу смещения

Испускание лучей в вершины

Освещение видимой области

Сортировка точек пересечения

Испускание лучей с небольшим смещением

Круг видимости и фонарик

А как насчёт окружностей?

Точка пересечения окружности и луча

Испускание лучей на окружности

Способы оптимизации

Пространственные хэш-карты

Линия сверхпокрытия на основе алгоритма Брезенхэма

Всё имеет свой конец

Длины отрезков: как сравнить и найти середину или концы единичного отрезка координатной прямой, правила об этом и примеры на рисунке

Метод наложения

Измерение длин:

Как сравнить 2 отрезка: способы решения задачи

Что такое отрезок

Сравнение двух отрезков

Вывод

Прямая и отрезок, измерение и сравнение отрезков

Отрезок

Сравнение отрезков

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Способы сравнения двух отрезков

Измерение длины

Наложение друг на друга

Геометрия 7 класс.Точка, прямая и отрезок

Как обозначить прямую

Решение задачи

Сколько общих точек имеют две прямые

Первый случай расположения прямых

Второй случай расположения прямых

Третий случай расположения прямых

Решение задачи

Что такое отрезок

Отрезок

Длина отрезка

Равные отрезки

Сравнение отрезков

Видеоурок «Сравнение отрезков и углов. Измерение отрезков»

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Способы сравнения двух отрезков

Измерение длины

Наложение друг на друга

Примеры

Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Многоугольник — это замкнутая ломанная линия

Урок 3 Получить доступ за 50 баллов Отрезок. Длина отрезка

А вот еще несколько наших интересных статей:

Поделиться этой статьей с друзьями:

Геометрия 7 класс. Урок 21.
Самостоятельная работа № 6 (задания)

Самостоятельная работа № 6
Указания к решению и ОТВЕТЫ