Сантиметр квадратный как пишется

Величина- это свойство объекта, явления, процесса, которое характеризуются количественно.

Любая величина имеет свое значение.

Значение величины выражается некоторым числом (размером) с указанием единицы измерения.

Единицей измерения величины является некоторая мера, числовое значение, которой равно единице.

На этом уроке рассмотрим единицы измерения длины и площади.

Выясним область их применения.

Познакомимся с новыми единицами площади.

Узнаем, как связаны единицы площади между собой.

Разберем правила и способы измерения площадей.

Единицы, в которых измеряются величины, называются единицами измерения.

Одна и та же величина может быть выражена в разных единицах измерения.

Числовое значение величины непосредственно зависит от выбранной единицы измерения.

Вам уже хорошо известны такие единицы измерения длины, как:

1. Миллиметр— единица длины в системе СИ.

Русское обозначение: мм.

Международное обозначение: mm.

Наглядно представить миллиметр можно с помощью шкалы линейки.

Одному миллиметру равно расстояние между самыми маленькими делениями на линейке.

Миллиметры применяют в качестве стандартной единицы измерения длины практически во всех странах мира (единица длины в системе СИ).

Используют данную меру длины в тех случаях, когда необходима высокая точность измерений и вычислений.

На чертежах миллиметр является единицей измерения по умолчанию.

2. Сантиметр— единица длины в системе СИ.

Русское обозначение: см.

Международное обозначение: сm.

Наглядно представить сантиметр можно с помощью линейки: десять миллиметровых делений представляют собой один сантиметр.

Отрезок один сантиметр равен отрезку десять миллиметров.

1 см = 10 мм.

3. Дециметр— единица измерения длины в системе СИ.

Русское обозначение: дм.

Международное обозначение: dm.

Наглядно представить сантиметр можно на сантиметровой линейке как отрезок равный десяти сантиметрам.

В одном дециметре содержится десять сантиметров или сто миллиметров.

1 дм = 10 см = 100 мм.

На практике дециметр используется не часто.

 4. Метр— мера длины, основная в системе СИ.

Русское обозначение: м.

Международное обозначение: m.

Отрезок в один метр равен отрезку десять дециметров.

1 м = 10 дм.

Каждые десять дециметров содержат по десять сантиметров, значит

1 м = 100 см.

С помощью обычной школьной линейки представить метр затруднительно.

Метр легко отмерить с помощью рулетки или портновской сантиметровой ленты.

5. Километр— широко используемая единица измерения длины, расстояния.

Русское обозначение: км.

Международное обозначение: km.

«Кило» от греческого тысяча, а «километр» — значит тысяча и метр.

В одном километре тысяча метров.

1 км = 1000 м.

Трудно наглядно изобразить километр, так как это большая мера длины.

В километрах измеряют обычно расстояния между населенными пунктами, странами, протяженность рек и морей, материков, островов и др.

Длина — это характеристика линейных размеров объекта.

Для вычисления площади необходимо знать эти линейные размеры.

Так для нахождения площади прямоугольника нужно знать длины его сторон.

Всем хорошо известно, что площадь прямоугольника равна произведению его длины и ширины.

Так как длина и ширина выражаются в линейных единицах, то их произведение будет представлять собой квадратную меру длины.

Таким образом, площадь измеряется в квадратных единицах измерения длины.

К основным единицам площади относят: квадратный километр, квадратный метр, квадратный дециметр, квадратный сантиметр, квадратный миллиметр.

Рассмотрим кратко каждую из них.

Вспомним, что квадрат- это прямоугольник, у которого все стороны равны.

Квадратная единица представляет собой единичный квадрат, у которого сторона равна единице измерения длины.

Площадь такого квадрата равна одной единице измерения длины во второй степени (т.е. возведенная в квадрат).

1. Квадратный миллиметр представляет собой квадрат со стороной в один миллиметр (1 мм).

Русское обозначение: мм².

Международное обозначение: mm².

S = 1 мм ∙ 1мм = 1 мм².

Квадратный миллиметр используют для измерения площадей маленьких поверхностей.

В квадратных миллиметрах измеряют, например, чипы микропроцессоров, площадь сечения провода, проволоки и т.д.

Для начертания и измерения объектов небольшой площади удобно использовать миллиметровую бумагу.

2. Квадратный сантиметр— это площадь квадрата, сторона которого равна один сантиметр (1 см).

Русское обозначение: см².

Международное обозначение: сm².

S = 1 см ∙ 1см = 1 см².

Квадратный сантиметр довольно часто применяют как единицу измерения площади фигур в школьной программе, так как квадратные сантиметры позволяют выражать небольшие по значению площади, соизмеримые с листом бумаги.

Легко представить и приближенно изобразить квадратный сантиметр на тетрадном листе в клетку: 2 клетки ≈ 1 см, поэтому квадрат, состоящий из четырех клеток, будет изображать 1 см².

3. Квадратный дециметр— это площадь квадрата, сторона которого равна один дециметр (1 дм).

Русское обозначение: дм².

Международное обозначение: dm².

S = 1 дм ∙ 1 дм = 1 дм².

На практике квадратный дециметр не используют, практически не используют его и в быту.

Квадратный дециметр можно встретить при решении некоторых математических задач, он существует как промежуточная единица между квадратным сантиметром и квадратным метром.

Дециметр квадратный можно приблизительно изобразить на тетрадном листе.

2 клетки ≈ 1 см.

10 см = 1 дм.

20 клеток ≈ 1 дм.

Следовательно, квадрат со стороной 20 тетрадных клеток будет изображать 1 дм².

4. Квадратный метр— это площадь квадрата со стороной один метр (1 м).

Русское обозначение: м².

Международное обозначение: m².

S = 1 м ∙ 1 м = 1 м².

Квадратный метр- это основная и самая распространенная единица площади в Международной системе СИ.

Часто используется для оценки площадей зданий и различных помещений (жилых, офисных, производственных), применяют в сельском хозяйстве, науке и технике, архитектуре, строительстве, в разных областях знаний: физике, медицине, географии и т.д.

Практически ни один ремонт не обходится без вычисления площади, причем эту площадь чаще всего приходится вычислять в метрах квадратных.

Необходимо знать и уметь высчитывать площадь стен, пола, потолка, окон и т.д. при закупке строительных материалов.

Наглядно представить один метр квадратный можно, вырезав из обоев квадрат со стороной в один метр.

5. Квадратный километр— площадь квадрата со стороной один километр (1 км).

Русское обозначение: км².

Международное обозначение: km².

S = 1 км ∙ 1 км = 1 км².

Для измерения больших площадей используют квадратный километр.

В квадратных километрах измеряют площади крупных объектов: городов, стран, континентов, озер, морей, океанов, планет и т.д.

У меня есть дополнительная информация к этой части урока!

Закрыть

Приведем примеры нескольких объектов, площади которых измеряются в квадратных километрах.

Площадь Мирового океана 361260000 км².

Мировой океан- это водная поверхность Земли, которая окружает континенты, острова и т.д.

Самый большой по площади и древний из всех океанов является Тихий океан.

Площадь Тихого океана оценивают в 178684000 км².

Он составляет почти половину всей площади Мирового океана.

Площадь поверхности планета Земля составляет 510072000 км².

Самым большим государством по величине территории является Россия, ее площадь составляет 17102345 км².

Площадь России приблизительно равна площади поверхности планеты Плутон.

Самым большим по площади городом является Нью-Йорк (США), он занимает 11875 км².

Крупнейшим озером в России является озеро Байкал, площадь его свободной поверхности воды составляет около 31500 км², это по площади сравнимо с государством Бельгия.

Озеро Байкал является самым глубоким озером на Земле.

Площадь, выраженную в квадратных километрах, используют при расчетах плотности населения.

Так как плотность населения- это количество людей (число жителей) на 1 км² площади

Кроме основных единиц измерения площадей существуют единицы для измерения площадей земельных участков.

К таким единицам относятся Гектар и Ар.

Ар— это внесистемная единица площади, равная 100 квадратным метрам, т.е. это квадрат со стороной в 10 м.

Ар от латинского «area»- площадь, поверхность.

Обозначение: а.

S = 10 м ∙ 10 м = 100 м² = а.

Ар в некоторых странах называют иначе.

В России ар имеет второе название (разговорное)- «сотка» (так как ар равен сотне квадратных метров).

Пример.

2 сотки- это 2 ар.

9 соток- это 9 ар и т.д.

Используют данную единицу площади в сельском и лесном хозяйстве для измерения небольших земельных и лесных участков.

Гектар— единица измерения площади, равная площади квадрата со стороной 100 м.

Русское обозначение: га.

Международное обозначение: ha.

Такое обозначение было принято Международным комитетом мер и весов в 1879 году.

На сегодняшний день гектар допущен в качестве единицы измерения площади вместе с единицами измерения системы СИ.

Гектар от латинского «гекто» и «ар» означает «сто» и «ар» соответственно.

S = 100 м ∙ 100 м = 10000 м² = га.

1 га = 100 ар = 100 соток.

Используют для обозначения площади больших участков земли: сельскохозяйственных угодий, лесов, полей.

До введения гектара в России использовали другие меры площади, например, десятина (примерно равная гектару).

У меня есть дополнительная информация к этой части урока!

Закрыть

Старинные меры площади.

Необходимость измерять и вычислять возникла с очень давних пор.

Измерительные и вычислительные навыки требовались в строительстве, земледелии, торговле и т.д.

В настоящее время современные единицы измерения однозначны и понятны человеку.

А в старые добрые времена не существовало четкой, структурированной и однозначной системы мер.

Подобная ситуация складывалась не только на Руси, но и в других странах.

На протяжении долгого периода времени единицы измерения были произвольными.

За единицу измерения принималось то, что находилось вокруг человека.

Часто в качестве единиц измерения использовали собственные части тела.

Такие меры были удобны, так как «измерительный инструмент» всегда был при себе, и воспользоваться им можно было в любой удобный момент.

Однако части тела у разных людей имеют различные размеры, следовательно, и единицы измерения были непостоянны, каждый раз меняли свои значения.

Например, русская старинная мера длины- аршин (расстояние между большим пальцем и указательным) непосредственно зависели от размеров руки, ведь рука взрослого мужчины значительно отличается от руки женщины.

В то время в торговые лавки приказчиками нанимали маленьких мужчин, таким образом купцы пытались экономить ткань, благодаря небольшим меркам.

Порой единицей измерения длины считали дальность полета брошенного камня, пушечный выстрел, дальность полета стрелы и др.

Порой длину меряли расстоянием, на которое был слышен крик петуха или бычий рев.

Часто требовалось измерять не только длины, но и площади различных объектов.

В основном такими объектами были земельные участки.

Измерение и вычисление площадей- это была и есть одна из важнейших практических задач.

Единицы измерения площадей были так же произвольными и неоднозначными.

Например, в Индии единицей измерения площади считался участок земли, который занимал загон для овец.

В Америке индейцы при покупке земельного участка принимали за меру площади, территорию, которую человек мог оббежать за один день, в связи с этим покупатель нанимал самого быстрого бегуна.

В Англии площадь своих земель измеряли работой быков, раньше акр (английская мера площади) представлял собой площадь участка земли, которую мог вспахать один бык за один день.

В Древней Руси мерой земельной площади был сельскохозяйственный инвентарь или объем трудовых ресурсов.

Например, в XI— XIII веках использовалась земельная мера плуг- мера площади земельного участка, с которой платили дань.

В XV— XVI веках в Новгородской земле для земельного налога применялась такая единица площади, как обжа — участок земли, который можно было вспахать на одной лошади за день.

Долгое время на Руси применяли для земельного налога такую меру площади как соха.

Она имела переменное значение, зависела от качества земли (с хороших земель значение ее было меньше) и от социального положения владельца земельного участка.

Для определения сенокосных угодий применяли «урожайные меры», например, таковой являлась «копна» единица измерения площади покоса.

Для пахотных земель использовали различные меры площади.

Примерно с XVI века появились в качестве основных мер земельных площадей десятина и четверть.

«Десятина»- единица земельной площади, которая представляла собой прямоугольник, стороны которого были или 80 на 30 саженей, или 60 на 40 саженей.

Такая «десятина» называлась «казенная десятина», равнялась 2400 квадратным саженям, ее использовали до введения метрической системы.

Через «десятину» выражались все другие меры площади.

Например, считалось, что с «десятины» снимали 10 «копен» сена.

«Четверть»- это половина «десятины», это площадь земли, на которую высевали меру объема ржи (четверть кади).

Кадью называли кадку, старинная мера сыпучих тел

Единицы измерения площади можно переводить из одной единицы в другую.

Например, чтобы найти сколько в квадратном сантиметре (1 см²) содержится квадратных миллиметров, необходимо вспомнить, сколько в одном сантиметре (1 см) миллиметров.

Известно, что 1 см²— это квадрат со стороной в 1 см.

1 см = 10 мм.

Тогда все четыре стороны имеют длину равную 10 мм.

Вычислим площадь квадрата со стороной 10 мм, для этого умножим длину квадрата (равную 10 мм) на его ширину (равную 10 мм), т.е. возведем число 10 в квадрат.

S = 10 мм ∙ 10 мм = 10² мм² = 100 мм².

Получаем: на один квадратный сантиметр приходится сто квадратных миллиметров.

1 см² = 100 мм²

В таком случае, чтобы перевести квадратные сантиметры в квадратные миллиметры, необходимо количество квадратных сантиметров умножить на 100.

Пример 1.

Переведем 4 см² в квадратные миллиметры.

Так как 1 см²— это 100 мм², то число квадратных миллиметров в 100 раз больше, чем число квадратных сантиметров, следовательно, умножим 4 см² на 100.

Решение:

4 см² = 4 ∙ 100 = 400 мм².

Ответ: 4 см² = 400 мм².

Соответственно, чтобы перевести квадратные миллиметры в квадратные сантиметры, нужно количество квадратных миллиметров разделить на 100.

Пример 2.

Выразим 400 мм² в квадратных сантиметрах.

Так как 100 мм²— это 1 см², выясним сколько будет содержаться квадратных сантиметров (1 см² = 100 мм²) в 400 мм².

Разделим 400 мм² на 100.

Решение:

400 мм² = 400 ÷ 100 = 4 см².

Ответ: 400 мм² = 4 см².

Рассуждая по такому принципу, можно установить взаимосвязь других единиц измерения площади.

Для этого необходимо четко знать и помнить соотношения единиц измерения длины.

1 см = 10 мм

1 дм = 10 см = 100 мм

1 м = 10 дм = 100 см = 1000 мм

1 км = 1000 м

Запишем соотношение единиц площади:

Пример 3.

Площадь лесного участка составляет 40 га.

Выразим данную площадь в м².

Решение:

1 га- это квадрат площадью 10000 м², значит 40 га- это 40 квадратов каждый площадью 10000 м², а это значит:

40 га = 40 ∙ 10000 = 400000 м².

Ответ: 40 га = 400000 м².

Пример 4.

Площадь распаханного поля составляет 5 ар.

Выразим данную площадь поля в м².

Решение:

1 ар- это квадрат площадью 100 м², значит, 5 ар- это 5 квадратов площадью 100 м² каждый, а это значит:

5 а = 5 ∙ 100 = 500 м².

Ответ: 5 а = 500 м².

Иначе можно сказать так: площадь распаханного поля составляет 5 соток.

Пример 5.

Выразим 2 м²14 см² в квадратных сантиметрах.

Решение:

Так как 1 м² = 10000 см², то 2 м² = 20000 см².

20000 см² да еще 14 см² получаем:

2 м²14 см² = 20000 см² + 14 см² = 20014 см²

Ответ: 2 м²14 см² = 20014 см²

Пример 6.

На рисунке изображен прямоугольник ABCD со сторонами 16 см и 2 м 20 см.

Найдем площадь прямоугольника ABCD.

Если стороны прямоугольника выражены в разных единицах измерения, то для вычисления площади необходимо длины сторон этого прямоугольника перевести в одинаковые единицы измерения.

Переведем длину и ширину прямоугольника ABCD в сантиметры.

Ширина прямоугольника а = 16 см уже выражена в сантиметрах.

Длину прямоугольника b = 2 м 20 см выразим в сантиметрах.

Так как 1 м = 100 см, то 2 м = 200 см.

200 см да еще 20 см получаем:

b = 200 см + 20 см = 220 см

Умение измерять и высчитывать площадь различных объектов- очень ценное знание, которое используется во многих сферах нашей жизни.

Например, часто приходится давать оценку земельных участков различного назначения.

В таком случае площадь может быть определена по результатам обмера участка в реальности, а также по планам и картам.

У меня есть дополнительная информация к этой части урока!

Закрыть

В зависимости от условий местности, требуемой точности измерения и наличия плана или карты существует несколько способов определения площадей.

1. При прямолинейных границах площади используют:

• Аналитический способ определения площади

Площадь вычисляют по результатам измерений координат вершин многоугольника, изображенного на плане (карте) с помощью специальных формул аналитической геометрии и компьютерных программ.

При этом участок разбивается на правильные геометрические фигуры.

• Геометрический способ определения площади

Площадь вычисляют по результатам измерений местности с помощью специальных измерительных приборов- дальномеров (лазерных, оптических), измеряющих расстояние от наблюдателя до объекта.

По специальным расчетным формулам, разбив измеряемую площадь на простые фигуры, высчитывают ее значение.

2. При произвольной форме границ участка используют:

• Графический способ определения площади (способ палеток)

Палетка- это прозрачная пластина, на которой нанесена сеть квадратов одинаковой площади.

Палетку накладывают на план (карту) измеряемого объекта и подсчитывают количество полных квадратов и неполных, попавших в контур измеряемого объекта, и вычисляют площадь.

• Механический способ определения площади

С помощью измерительного прибора планиметра по плану или карте определяют площадь участков произвольной формы

Для того чтобы измерить площадь помещения, нет необходимости совершать сложные вычислительные операции и иметь специальные измерительные приборы.

Измерение площади в таком случае сводится к измерению рулеткой длины отрезков, ограничивающих эту площадь.

Чаще всего помещение имеет прямоугольную или квадратную форму, вычислить площадь такой фигуры несложно.

Необходимо измерить длину и ширину помещения (в одинаковых единицах измерения) и перемножить полученные значения.

Для расчета применяется формула: S = а ∙ b

S— площадь помещения

а— ширина помещения

b— длина помещения

Если же необходимо определить площадь сложной формы, то измерением просто длины и ширины помещения не обойтись.

Известно, что общая площадь фигуры равна сумме площадей ее частей.

S = S₁ + S₂ + S₃…

В таком случае необходимо измеряемое пространство разделить условно на прямоугольники и квадраты.

Определить площади каждой простой фигуры, затем сложить получившиеся значения площадей.

Рассмотрим пример.

Найдем площадь всей квартиры, изображенной на рисунке-плане.

Условно разобьем пространство всей квартиры на прямоугольники, у каждого найдем площадь.

S₁ = а₁ ∙ b₁— площадь кухни в м²

S₂ = а₂ ∙ b₂— площадь спальни в м²

S₃ = а₃ ∙ b₃— площадь гостиной в м²

S₄ = а₄ ∙ b₄— площадь прихожей в м²

S₅ = а₅ ∙ b₅— площадь ванной комнаты в м².

S— общая площадь квартиры, ее найдем, сложив площади каждой комнаты

S= S₁ + S₂ + S₃ + S₄ + S₅

Рассмотрим решение нескольких практических задач.

Задача №1.

Определите сколько стоит жалюзи на окно шириной 2 м и высотой 2 м, если цена жалюзи 600 рублей за 1 м².

Пусть а— ширина окна, b— длина окна, р— цена жалюзи за 1 м².

Задача №2.

Линолеум стоит 300 рублей за 1 м².

Определите стоимость линолеума, который необходимо купить, чтобы застелить пол в комнате шириной 4 м и длинной 6 м.

Пусть а— ширина комнаты, b— длина комнаты, р— цена линолеума за 1 м².

Задача №3

Сколько банок краски потребуется для покраски стены длинной 4 м шириной 3 м, если на 1 м² требуется 250 г краски.

Краска продается в банках по 3000 г.

Выясним, какую площадь необходимо покрасить и сколько на это понадобится граммов краски.

Разделим общее количество необходимой краски на массу одной банки, получим число банок, которые нужно купить для покраски стены.

Пусть m— масса краски, которая расходуется на 1 м²

m_б— масса одной банки с краской

m_с— масса краски, которая необходима для покраски всей стены

n— число банок с краской, которые нужно купить для покраски стены

Если бы в стене был оконный или дверной проем, то необходимо было бы высчитать площадь окна (двери) и вычесть это значение из общей площади стены, которая подлежит покраске.

Пройти тест

Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия

Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Физическая … Википедия

Физическая величина это количественная характеристика объекта или явления в физике, либо результат измерения. Размер физической величины количественная определенность физической величины, присущая конкретному материальному объекту, системе,… … Википедия

У этого термина существуют и другие значения, см. Фотон (значения). Фотон Символ: иногда … Википедия

У этого термина существуют и другие значения, см. Борн. Макс Борн Max Born … Википедия

Примеры разнообразных физических явлений Физика (от др. греч. φύσις … Википедия

Фотон Символ: иногда Излученные фотоны в когерентном луче лазера. Состав: Семья … Википедия

У этого термина существуют и другие значения, см. Масса (значения). Масса Размерность M Единицы измерения СИ кг … Википедия

CROCUS Ядерный реактор это устройство, в котором осуществляется управляемая цепная ядерная реакция, сопровождающаяся выделением энергии. Первый ядерный реактор построен и запущен в декабре 1942 года в … Википедия

Книги

• Гидравлика. Учебник и практикум для академического бакалавриата , Кудинов В.А.. В учебнике изложены основные физико-механические свойства жидкостей, вопросы гидростатики и гидродинамики, даны основы теории гидродинамического подобия и математического моделирования…
• Гидравлика 4-е изд., пер. и доп. Учебник и практикум для академического бакалавриата , Эдуард Михайлович Карташов. В учебнике изложены основные физико-механические свойства жидкостей, вопросы гидростатики и гидродинамики, даны основы теории гидродинамического подобия и математического моделирования…

ГОСУДАРСТВЕННАЯ
СИСТЕМА ОБЕСПЕЧЕНИЯ
ЕДИНСТВА ИЗМЕРЕНИЙ

ЕДИНИЦЫ
ФИЗИЧЕСКИХ ВЕЛИЧИН

ГОСТ 8.417-81

(СТ СЭВ 1052-78)

ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР ПО СТАНДАРТАМ

Москва

РАЗРАБОТАН
Государственным
комитетом СССР по стандартам ИСПОЛНИТЕЛИ
Ю.В. Тарбеев
,д-р
техн. наук; К.П. Широков
,д-р техн. наук; П.Н. Селиванов
,
канд. техн. наук; Н.А. Ерюхина
ВНЕСЕН
Государственным
комитетом СССР по стандартам Член Госстандарта
Л.К. Исаев
УТВЕРЖДЕН И
ВВЕДЕН В ДЕЙСТВИЕ
Постановлением Государственного комитета СССР по
стандартам от 19 марта 1981 г. № 1449

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

Государственная система обеспечения единства измерений ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН State system for ensuring the uniformity of measurements. Units of physical quantities

ГОСТ 8.417-81 (СТ СЭВ 1052-78 )

Постановлением
Государственного комитета СССР по стандартам от 19 марта 1981 г. № 1449 срок
введения установлен

с 01.01 1982 г.

Настоящий
стандарт устанавливает единицы физических величин (далее — единицы),
применяемые в СССР, их наименования, обозначения и правила применения этих
единиц Стандарт не
распространяется на единицы, применяемые в научных исследованиях и при
публикациях их результатов, если в них не рассматривают и не используют
результаты измерений конкретных физических величин, а также на единицы величин,
оцениваемых по условным шкалам*. * Под условными шкалами понимаются, например, шкалы
твердости Роквелла и Виккерса, светочувствительности фотоматериалов. Стандарт
соответствует СТ СЭВ 1052-78 в части общих положений, единиц Международной
системы, единиц, не входящих в СИ, правил образования десятичных кратных и
дольных единиц, а также их наименований и обозначений, правил написания
обозначений единиц, правил образования когерентных производных единиц СИ (см.
справочное приложение 4).

1.1. Подлежат обязательному применению единицы Международной
системы единиц*, а также десятичные кратные и дольные от них (см. разд. 2 настоящего
стандарта). * Международная система единиц (международное сокращенное
наименование — SI , в русской транскрипции — СИ), принята в 1960 г. XI Генеральной конференцией по мерам
и весам (ГКМВ) и уточнена на последующих ГКМВ. 1.2. Допускается применять наравне с единицами по п. 1.1 единицы, не входящие
в СИ, в соответствии с пп. 3.1 и 3.2 , их сочетания с единицами СИ, а также некоторые нашедшие
широкое применение на практике десятичные кратные и дольные от
вышеперечисленных единиц. 1.3. Временно
допускается применять наравне с единицами по п. 1.1 единицы, не входящие в СИ, в соответствии с п. 3.3, а также некоторые, получившие
распространение на практике кратные и дольные от них, сочетания этих единиц с
единицами СИ, десятичными кратными и дольными от них и с единицами по п. 3.1. 1.4. Во вновь
разрабатываемой или пересматриваемой документации, а также публикациях значения
величин должны выражаться в единицах СИ, десятичных кратных и дольных от них и
(или) в единицах, допускаемых к применению в соответствии с п. 1.2. Допускается
также в указанной документации применять единицы по п. 3.3, срок изъятия которых будет установлен в соответствии
с международными соглашениями. 1.5. Во вновь
утверждаемой нормативно-технической документации на средства измерений должна
предусматриваться их градуировка в единицах СИ, десятичных кратных и дольных от
них или в единицах, допускаемых к применению в соответствии с п. 1.2. 1.6. Вновь
разрабатываемая нормативно-техническая документация по методам и средствам
поверки должна предусматривать поверку средств измерений, проградуированных во
вновь вводимых единицах. 1.7. Единицы СИ,
установленные настоящим стандартом, и единицы, допускаемые к применению пп. 3.1 и 3.2, должны применяться в учебных процессах всех учебных
заведений, в учебниках и учебных пособиях. 1.8. Пересмотр
нормативно-технической, конструкторской, технологической и другой технической
документации, в которой применяются единицы, не предусмотренные настоящим
стандартом, а также приведение в соответствие с пп. 1.1 и 1.2
настоящего стандарта средств измерений, градуированных в единицах, подлежащих
изъятию, осуществляют в соответствии с п. 3.4
настоящего стандарта. 1.9. При
договорно-правовых отношениях по сотрудничеству с зарубежными странами, при
участии в деятельности международных организаций, а также в поставляемой за
границу вместе с экспортной продукцией (включая транспортную и потребительскую
тару) технической и другой документации, применяют международные обозначения
единиц. В документации на
экспортную продукцию, если эта документация не отправляется за границу,
допускается применять русские обозначения единиц. (Новая редакция,
Изм. № 1).
1.10. В нормативно-технической
конструкторской, технологической и другой технической документации на различные
виды изделий и продукции, используемые только в СССР, применяют предпочтительно
русские обозначения единиц. При этом независимо от того, какие обозначения
единиц использованы в документации на средства измерений при указании единиц
физических величин на табличках, шкалах и щитках этих средств измерений
применяют международные обозначения единиц. (Новая редакция,
Изм. № 2).
1.11. В печатных
изданиях допускается применять либо международные, либо русские обозначения
единиц. Одновременно применение обоих видов обозначений в одном и том же
издании не допускается, за исключением публикаций по единицам физических
величин.

2.1. Основные
единицы СИ приведены в табл. 1.

Таблица 1

Величина
Наименование	Размерность	Наименование	Обозначение		Определение
			международное
Длина					Метр есть длина пути, проходимого светом в вакууме за интервал времени 1/299792458 S [ XVII ГКМВ (1983 г.), Резолюция 1].
Масса		килограмм			Килограмм есть единица массы, равная массе международного прототипа килограмма [ I ГКМВ (1889 г.) и III ГКМВ (1901 г)]
Время					Секунда есть время, равное 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 [ XIII ГКМВ (1967 г.), Резолюция 1]
Сила электрического тока					Ампер есть сила равная силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 m один от другого, вызвал бы на каждом участке проводника длиной 1 m силу взаимодействия, равную 2 × 10 -7 N [МКМВ (1946 г.), Резолюция 2, одобренная IX ГКМВ (1948 г.)]
Термодинамическая температура					Кельвин есть единица термодинамической температуры, равная 1/273,16 части термодинамической температуры тройной точки воды [Х III ГКМВ (1967 г.), Резолюция 4]
Количество вещества					Моль есть количество вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 kg . При применении моля структурные элементы должны быть специфицированы и могут быть атомами, молекулами, ионами, электронами и другими частицами или специфицированными группами частиц [ XIV ГКМВ (1971 г.), Резолюция 3]
Сила света					Кандела есть сила, равная силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540 × 10 12 Hz , энергетическая сила света которого в этом направлении составляет 1/683 W / sr [ XVI ГКМВ (1979 г.), Резолюция 3]
Примечания: 1. Кроме температуры Кельвина (обозначение Т ) допускается применять также температуру Цельсия (обозначение t ), определяемую выражением t = T — Т 0 , где Т 0 = 273,15 К, по определению. Температура Кельвина выражается в Кельвинах, температура Цельсия — в градусах Цельсия (обозначение международное и русское °С). По размеру градус Цельсия равен кельвину. 2. Интервал или разность температур Кельвина выражают в кельвинах. Интервал или разность температур Цельсия допускается выражать как в кельвинах, так и в градусах Цельсия. 3. Обозначение Международной практической температуры в Международной практической температурной шкале 1968 г., если ее необходимо отличить от термодинамической температуры, образуется путем добавления к обозначению термодинамической, температуры индекса «68» (например, Т 68 или t 68). 4. Единство световых измерений обеспечивается в соответствии с ГОСТ 8.023-83.

(Измененная
редакция, Изм. № 2, 3).
2.2.
Дополнительные единицы СИ приведены в табл. 2.

Таблица 2

Наименование величины
	Наименование	Обозначение		Определение
		международное
Плоский угол				Радиан есть угол между двумя радиусами окружности, длина дуги между которыми равна радиусу
Телесный угол	стерадиан			Стерадиан есть телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы

(Измененная
редакция, Изм. № 3).
2.3. Производные
единицы СИ следует образовывать из основных и дополнительных единиц СИ по
правилам образования когерентных производных единиц (см. обязательное
приложение 1). Производные
единицы СИ, имеющие специальные наименования, также могут быть использованы для
образования других производных единиц СИ. Производные единицы, имеющие
специальные наименования, и примеры других производных единиц приведены в табл.
3 — 5. Примечание. Электрические и магнитные
единицы СИ следует образовывать в соответствии с рационализованной формой
уравнений электромагнитного поля.

Таблица 3

Примеры производных единиц СИ, наименования которых образованы из наименований
основных и дополнительных единиц

Величина
Наименование	Размерность	Наименование	Обозначение
			международное
Площадь		квадратный метр
Объем, вместимость		кубический метр
Скорость		метр в секунду
Угловая скорость		радиан в секунду
Ускорение		метр на секунду в квадрате
Угловое ускорение		радиан на секунду в квадрате
Волновое число		метр в минус первой степени
Плотность		килограмм на кубический метр
Удельный объем		кубический метр на килограмм
		ампер на квадратный метр
		ампер на метр
Молярная концентрация		моль на кубический метр
Поток ионизирующих частиц		секунда в минус первой степени
Плотность потока частиц		секунда в минус первой степени — метр в минус второй степени
Яркость		кандела на квадратный метр

Таблица 4

Производные единицы
СИ, имеющие специальные наименования

Величина
Наименование	Размерность	Наименование	Обозначение		Выражение через основные и дополнительные, единицы СИ
			международное
Частота
Сила, вес
Давление, механическое напряжение, модуль упругости
Энергия, работа, количество теплоты					m 2 × kg × s -2
Мощность, поток энергии					m 2 × kg × s -3
Электрический заряд (количество электричества)
Электрическое напряжение, электрический потенциал, разность электрических потенциалов, электродвижущая сила					m 2 × kg × s -3 × A -1
Электрическая емкость	L -2 M -1 T 4 I 2				m -2 × kg -1 × s 4 × A 2
					m 2 × kg × s -3 × A -2
Электрическая проводимость	L -2 M -1 T 3 I 2				m -2 × kg -1 × s 3 × A 2
Поток магнитной индукции, магнитный поток					m 2 × kg × s -2 × A -1
Плотность магнитного потока, магнитная индукция					kg × s -2 × A -1
Индуктивность, взаимная индуктивность					m 2 × kg × s -2 × A -2
Световой поток
Освещенность					m -2 × cd × sr
Активность нуклида в радиоактивном источнике (активность радионуклида)		беккерель
Поглощенная доза излучения, керма, показатель поглощенной дозы (поглощенная доза ионизирующего излучения)
Эквивалентная доза излучения

(Измененная
редакция, Изм. № 3).

Таблица 5

Примеры производных
единиц СИ, наименования которых образованы с использованием специальных
наименований, приведенных в табл. 4

Величина
Наименование	Размерность	Наименование	Обозначение		Выражение через основные и дополнительные единицы СИ
			международное
Момент силы		ньютон-метр			m 2 × kg × s -2
Поверхностное натяжение		Ньютон на метр
Динамическая вязкость		паскаль-секунда			m -1 × kg × s -1
		кулон на кубический метр
Электрическое смещение		кулон на квадратный метр
		вольт на метр			m × kg × s -3 × A -1
Абсолютная диэлектрическая проницаемость	L -3 M -1 × T 4 I 2	фарад на метр			m -3 × kg -1 × s 4 × A 2
Абсолютная магнитная проницаемость		генри на метр			m × kg × s -2 × A -2
Удельная энергия		джоуль на килограмм
Теплоемкость системы, энтропия системы		джоуль на кельвин			m 2 × kg × s -2 × K -1
Удельная теплоемкость, удельная энтропия		джоуль на килограмм-кельвин		Дж/(кг × К)	m 2 × s -2 × K -1
Поверхностная плотность потока энергии		ватт на квадратный метр
Теплопроводность		ватт на метр-кельвнн			m × kg × s -3 × K -1
		джоуль на моль			m 2 × kg × s -2 × mol -1
Молярная энтропия, молярная теплоемкость	L 2 MT -2 q -1 N -1	джоуль на моль-кельвин		Дж/(моль × К)	m 2 × kg × s -2 × K -1 × mol -1
		ватт на стерадиан			m 2 × kg × s -3 × sr -1
Экспозиционная доза (рентгеновского и гамма-излучения)		кулон на килограмм
Мощность поглощенной дозы		грэй в секунду

3.1. Единицы, перечисленные в табл. 6 , допускаются к
применению без ограничения срока наравне с единицами СИ. 3.2. Без ограничения срока допускается применять относительные и
логарифмические единицы за исключением единицы непер (см. п. 3.3). 3.3. Единицы, приведенные в табл. 7 , временно
допускается применять до принятия по ним соответствующих международных решений. 3.4. Единицы, соотношения которых с единицами СИ даны в справочном
приложении 2 , изымаются из обращения в сроки, предусмотренные
программами мероприятий по переходу на единицы СИ, разработанными в
соответствии с РД 50-160-79 . 3.5. В
обоснованных случаях в отраслях народного хозяйства допускается применение
единиц, не предусмотренных настоящим стандартом, путем введения их в отраслевые
стандарты по согласованию с Госстандартом.

Таблица 6

Внесистемные единицы,
допускаемые к применению наравне с единицами СИ

Наименование величины					Примечание
	Наименование	Обозначение		Соотношение с единицей СИ
		международное
Масса
	атомная единица массы			1,66057 × 10 -27 × kg (приблизительно)
Время 1
				86400 s
Плоский угол				(p /180) rad = 1,745329… × 10 -2 × rad
				(p /10800) rad = 2,908882… × 10 -4 rad
				(p /648000) rad = 4,848137…10 -6 rad
Объем, вместимость
Длина	астрономическая единица			1,49598 × 10 11 m (приблизительно)
	световой год			9,4605 × 10 15 m (приблизительно)
				3,0857 × 10 16 m (приблизительно)
Оптическая сила	диоптрия
Площадь
Энергия	электрон-вольт			1,60219 × 10 -19 J (приблизительно)
Полная мощность	вольт-ампер
Реактивная мощность
Механическое напряжение	ньютон на квадратный миллиметр
1 Допускается также применять другие единицы, получившие широкое распространение, например неделя, месяц, год, век, тысячелетие и т.п. 2 Допускается применять наименование «гон» 3 Не рекомендуется применять при точных измерениях. При возможности смещения обозначения l с цифрой 1 допускается обозначение L . Примечание. Единицы времени (минуту, час, сутки), плоского угла (градус, минуту, секунду), астрономическую единицу, световой год, диоптрию и атомную единицу массы не допускается применять с приставками

(Измененная
редакция, Изм. № 3).

Таблица 7

Единицы, временно
допускаемые к применению

Наименование величины					Примечание
	Наименование	Обозначение		Соотношение с единицей СИ
		международное
Длина	морская миля			1852 m (точно)	В морской навигации
Ускорение					В гравиметрии
Масса				2 × 10 -4 kg (точно)	Для драгоценных камней и жемчуга
Линейная плотность				10 -6 kg / m (точно)	В текстильной промышленности
Скорость					В морской навигации
Частота вращения	оборот в секунду
	оборот в минуту			1/60 s -1 = 0,016(6) s -1
Давление
Натуральный логарифм безразмерного отношения физической величины к одноименной физической величине, принимаемой за исходную					1 Np = 0,8686…В = = 8,686… dB

(Измененная
редакция, Изм. № 3).

4.1. Десятичные кратные
и дольные единицы, а также их наименования и обозначения следует образовывать с
помощью множителей и приставок, приведенных в табл. 8.

Таблица 8

Множители и приставки для образования десятичных
кратных и дольных единиц и их наименований

Множитель	Приставка	Обозначение приставки		Множитель	Приставка	Обозначение приставки
		международное				международное

4.2.
Присоединение к наименованию единицы двух или более приставок подряд не
допускается. Например, вместо наименования единицы микромикрофарад следует
писать пикофарад. Примечания: 1 В связи с тем, что наименование
основной единицы — килограмм содержит приставку «кило», для образования кратных
и дольных единиц массы используется дольная единица грамм (0,001 kg , кг), и приставки надо
присоединять к слову «грамм», например, миллиграмм (mg , мг) вместо микрокилограмм (m kg , мккг). 2. Дольную единицу
массы — «грамм» допускается применять и без присоединения приставки. 4.3. Приставку
или ее обозначение следует писать слитно с наименованием единицы, к которой она
присоединяется, или соответственно, с ее обозначением. 4.4.
Если единица образована как произведение или отношение единиц, приставку
следует присоединять к наименованию первой единицы, входящей в произведение или
в отношение.
Допускается
применять приставку во втором множителе произведения или в знаменателе лишь в
обоснованных случаях, когда такие единицы широко распространены и переход к единицам,
образованным в соответствии с первой частью пункта, связан с большими
трудностями, например: тонна-километр (t × km ; т × км), ватт на
квадратный сантиметр (W / cm 2 ; Вт/см 2), вольт на
сантиметр (V / cm ; В/см), ампер на квадратный миллиметр (A / mm 2 ; А/мм 2). 4.5.
Наименования кратных и дольных единиц от единицы, возведенной в степень,
следует образовывать путем присоединения приставки к наименованию исходной
единицы, например, для образования наименований кратной или дольной единицы от
единицы площади — квадратного метра, представляющей собой вторую степень
единицы длины — метра, приставку следует присоединять к наименованию этой
последней единицы: квадратный километр, квадратный сантиметр и т.д. 4.6. Обозначения
кратных и дольных единиц от единицы, возведенной в степень, следует
образовывать добавлением соответствующего показателя степени к обозначению
кратной или дольной от этой единицы, причем показатель означает возведение в
степень кратной или дольной единицы (вместе с приставкой). Примеры: 1. 5 km 2 = 5(10 3
m) 2 = 5 × 10 6 m 2 . 2. 250 cm 3 /s = 250(10 -2 m) 3 /(1
s) = 250 × 10 -6
m 3 /s. 3. 0,002 cm -1 = 0,002(10 -2
m) -1 = 0,002 × 100 m -1 = 0,2 m -1 . 4.7.
Рекомендации по выбору десятичных кратных и дольных единиц приведены в справочном
приложении 3.

5.1. Для написания значений величин следует применять обозначения
единиц буквами или специальными знаками (…°,… ¢ ,… ¢ ¢), причем устанавливаются два вида буквенных обозначений:
международные (с использованием букв латинского или греческого алфавита) и
русские (с использованием букв русского алфавита). Устанавливаемые стандартом
обозначения единиц приведены в табл. 1 — 7 . Международные и
русские обозначения относительных и логарифмических единиц следующие: процент
(%), промилле (о / оо), миллионная доля (рр m , млн -1), бел (В, Б), децибел (dB , дБ), октава (-, окт), декада (-, дек), фон (phon , фон). 5.2. Буквенные
обозначения единиц должны печататься прямым шрифтом. В обозначениях единиц
точку как знак сокращения не ставят. 5.3. Обозначения
единиц следует применять после числовых: значений величин и помещать в строку с
ними (без переноса на следующую строку). Между
последней цифрой числа и обозначением единицы следует оставлять пробел, равный
минимальному расстоянию между словами, которое определено для каждого типа и
размера шрифта по ГОСТ
2.304-81.
Исключения составляют обозначения
в виде знака, поднятого над строкой (п. 5.1),
перед которыми пробела не оставляют.
(Измененная
редакция, Изм. № 3).
5.4.
При наличии десятичной дроби в числовом значении величины обозначение единицы следует
помещать после всех цифр.
5.5. При указании значений величин
с предельными отклонениями следует заключать числовые значения с предельными
отклонениями в скобки и обозначения единицы помешать после скобок или
проставлять обозначения единиц после числового значения величины и после ее
предельного отклонения.
5.6. Допускается
применять обозначения единиц в заголовках граф и в наименованиях строк
(боковиках) таблиц. Примеры:

Номинальный расход. m 3 / h	Верхний предел показаний, m 3		Цена деления крайнего правого ролика, m 3 , не более
100, 160, 250, 400, 600 и 1000
2500, 4000, 6000 и 10000
Тяговая мощность, kW
Габаритные размеры, mm:
длина
ширина
высота
Колея, mm
Просвет, mm

5.7. Допускается применять обозначения
единиц в пояснениях обозначений величин к формулам. Помещение обозначений
единиц в одной строке с формулами, выражающими зависимости между величинами или
между их числовыми значениями, представленными в буквенной форме, не
допускается.
5.8. Буквенные обозначения единиц,
входящих в произведение, следует отделять точками на средней линии, как знаками
умножения*.
* В машинописных текстах допускается точку не поднимать. Допускается
буквенные обозначения единиц, входящих в произведение, отделять пробелами, если
это не приводит к недоразумению. 5.9.
В буквенных обозначениях отношений единиц в качестве знака деления должна
применяться только одна черта: косая или горизонтальная. Допускается применять
обозначения единиц в виде произведения обозначений единиц, возведенных в
степени (положительные и отрицательные)**.
** Если для одной из единиц, входящих в отношение,
установлено обозначение в виде отрицательной степени (например s -1 , m -1 , К -1 ; c -1 , м -1 , К -1),
применять косую или горизонтальную черту не допускается. 5.10.
При применении косой черты обозначения единиц в числителе и знаменателе следует
помещать в строку, произведение обозначений единиц в знаменателе следует
заключать в скобки.
5.11. При указании производной
единицы, состоящей из двух и более единиц, не допускается комбинировать
буквенные обозначения и наименования единиц, т.е. для одних единиц приводить обозначения,
а для других — наименования.
Примечание. Допускается применять сочетания
специальных знаков…°,… ¢ ,… ¢ ¢ , % и о / оо с буквенными обозначениями единиц,
например…°/ s и т. д.

Обязательное

Когерентные
производные единицы (далее — производные единицы) Международной системы, как правило,
образуют при помощи простейших уравнений связи между величинами (определяющих
уравнений), в которых числовые
коэффициенты равны 1. Для образования производных единиц величины в уравнениях
связи принимают равными единицам СИ. Пример. Единицу скорости образуют с помощью уравнения, определяющего
скорость прямолинейно и равномерно движущейся точки

v
= s/t
,

Где v
— скорость; s
— длина пройденного пути; t
— время движения точки. Подстановка
вместо s
и t
их единиц СИ дает

[v
] = [s
]/[t
] = 1 m/s.

Следовательно,
единицей скорости СИ является метр в секунду. Он равен скорости прямолинейно и
равномерно движущейся точки, при которой эта точка за время 1 s перемещается на расстояние 1 m . Если уравнение
связи содержит числовой коэффициент, отличный от 1, то для образования
когерентной производной единицы СИ в правую часть подставляют величины со
значениями в единицах СИ, дающими после умножения на коэффициент общее числовое
значение, равное числу 1. Пример. Если для образования единицы энергии используют уравнение

Где Е
— кинетическая энергия; m — масса материальной точки; v
— скорость
движения точки, то когерентную
единицу энергии СИ образуют, например, следующим образом:

Следовательно,
единицей энергии СИ является джоуль (равный ньютон-метру). В приведенных
примерах он равен кинетической энергии тела массой 2 kg , движущегося со скоростью 1 m / s , или же тела массой 1 kg , движущегося со скоростью

Справочное

Наименование величины					Примечание
	Наименование	Обозначение		Соотношение с единицей СИ
		международное
Длина	ангстрем
	икс-единица			1,00206 × 10 -13 m (приблизительно)
Площадь
Масса
Телесный угол	квадратный градус			3,0462… × 10 -4 sr
Сила, вес
	килограмм-сила			9,80665 N (точно)
	килопонд
	грамм-сила			9,83665 × 10 -3 N (точно)
	тонна-сила			9806,65 N (точно)
Давление	килограмм-сила на квадратный сантиметр			98066,5 Ра (точно)
	килопонд на квадратный сантиметр
	миллиметр водяного столба		мм вод. ст.	9,80665 Ра (точно)
	миллиметр ртутного столба		мм рт. ст.
Напряжение (механическое)	килограмм-сила на квадратный миллиметр			9,80665 × 10 6 Ра (точно)
	килопонд на квадратный миллиметр			9,80665 × 10 6 Ра (точно)
Работа, энергия
Мощность	лошадиная сила
Динамическая вязкость
Кинематическая вязкость
	ом-квадратный миллиметр на метр		Ом × мм 2 /м
Магнитный поток	максвелл
Магнитная индукция
	гпльберт			(10/4 p) А = 0,795775…А
Напряженность магнитного поля				(10 3 / p) А/ m = 79,5775…А/ m
Количество теплоты, термодинамический потенциал (внутренняя энергия, энтальпия, изохорно-изотермический потенциал), теплота фазового превращения, теплота химической реакции	калория (межд.)			4,1858 J (точно)
	калория термохимическая			4,1840 J (приблизительно)
	калория 15-градусная			4,1855 J (приблизительно)
Поглощенная доза излучения
Эквивалентная доза излучения, показатель эквивалентной дозы
Экспозиционная доза фотонного излучения (экспозиционная доза гамма- и рентгеновского излучений)				2,58 × 10 -4 C / kg (точно)
Активность нуклида в радиоактивном источнике				3,700 × 10 10 Bq (точно)
Длина
Угол поворота				2 p rad = 6,28… rad
Магнитодвижущая сила, разность магнитных потенциалов	ампервиток
Яркость
Площадь

Измененная
редакция, Изм. № 3.

Справочное

1. Выбор десятичной кратной или дольной единицы от единицы СИ диктуется
прежде всего удобством ее применения. Из многообразия кратных и дольных единиц,
которые могут быть образованы при помощи приставок, выбирают единицу,
приводящую к числовым значениям величины, приемлемым на практике. В принципе
кратные и дольные единицы выбирают таким образом, чтобы числовые значения
величины находились в диапазоне от 0,1 до 1000. 1.1. В некоторых
случаях целесообразно применять одну и ту же кратную или дольную единицу, даже
если числовые значения выходят за пределы диапазона от 0,1 до 1000, например, в
таблицах числовых значений для одной величины или при сопоставлении этих
значений в одном тексте. 1.2. В некоторых
областях всегда используют одну и ту же кратную или дольную единицу. Например,
в чертежах, применяемых в машиностроении, линейные размеры всегда выражают в
миллиметрах. 2. В табл. 1 настоящего приложения приведены
рекомендуемые для применения кратные и дольные единицы от единиц СИ. Представленные в
табл. 1 кратные и дольные единицы от
единиц СИ для данной физической величины не следует считать исчерпывающими, так
как они могут не охватывать диапазоны физических величин в развивающихся и
вновь возникающих областях науки
и техники. Тем не менее, рекомендуемые кратные и дольные единицы от единиц СИ
способствуют единообразию представления значений физических величин,
относящихся к различным областям техники. В этой же таблице
помещены также получившие широкое распространение на практике кратные и дольные
единицы от единиц, применяемых наравне с единицами СИ. 3. Для величин,
не охваченных табл. 1, следует
использовать кратные и дольные единицы, выбранные в соответствии с п. 1 данного приложения. 4. Для снижения
вероятности ошибок при расчетах десятичные кратные и дольные единицы
рекомендуется подставлять только в конечный результат, а в процессе вычислений
все величины выражать в единицах СИ, заменяя приставки степенями числа 10. 5. В табл. 2 настоящего приложения приведены
получившие распространение единицы некоторых логарифмических величин.

Таблица 1

Наименование величины	Обозначения
	единиц СИ		единиц, не входящих и СИ	кратных и дольных от единиц, не входящих в СИ
Часть I . Пространство и время
Плоский угол	rad ; рад (радиан)	m rad ; мкрад	… ° (градус)… (минута)…» (секунда)
Телесный угол	sr ; cp (стерадиан)
Длина	m ; м (метр)		… ° (градус) … ¢ (минута) … ² (секунда)
Площадь
Объем, вместимость			l (L); л (литр)
Время	s ; с (секунда)		d ; сут (сутки) min ; мин (минута)
Скорость
Ускорение	m / s 2 ; м/с 2
Часть II . Периодические и связанные с ними явления
	Hz ; Гц (герц)
Частота вращения			min -1 ; мин -1
Часть III . Механика
Масса	kg ; кг (килограмм)		t ; т (тонна)
Линейная плотность	kg / m ; кг/м	mg / m ; мг/м или g / km ; г/км
Плотность	kg / m 3 ; кг/м 3	Mg / m 3 ; Мг/м 3 kg / dm 3 ; кг/дм 3 g / cm 3 ; г/см 3	t / m 3 ; т/м 3 или kg / l ; кг/л	g / ml ; г/мл
Количество движения	kg × m / s ; кг × м/с
Момент количества движения	kg × m 2 / s ; кг × м 2 /с
Момент инерции (динамический момент инерции)	kg × m 2 , кг × м 2
Сила, вес	N ; Н (ньютон)
Момент силы	N × m ; Н × м	MN × m ; МН × м kN × m ; кН × м mN × m ; мН × м m N × m ; мкН × м
Давление	Ра; Па (паскаль)	m Ра; мкПа
Напряжение
Динамическая вязкость	Ра × s ; Па × с	mPa × s ; мПа × с
Кинематическая вязкость	m 2 / s ; м 2 /с	mm 2 / s ; мм 2 /с
Поверхностное натяжение		mN / m ; мН/м
Энергия, работа	J ; Дж (джоуль)		(электрон-вольт)	GeV ; ГэВ MeV ; МэВ keV ; кэВ
Мощность	W ; Вт (ватт)
Часть IV . Теплота
Температура	К; К (кельвин)
Температурный коэффициент
Теплота, количество теплоты
Тепловой поток
Теплопроводность
Коэффициент теплопередачи	Вт/(м 2 × К)
Теплоемкость		kJ / K ; кДж/К
Удельная теплоемкость	Дж/(кг × К)	kJ /(kg × К); кДж/(кг × К)
Энтропия		kJ / K ; кДж/К
Удельная энтропия	Дж/(кг × К)	kJ /(kg × K); кДж/(кг × К)
Удельное количество теплоты	J / kg ; Дж/кг	MJ / kg ; МДж/кг kJ / kg ; кДж/кг
Удельная теплота фазового превращения	J / kg ; Дж/кг	MJ / kg ; МДж/кг kJ / kg ; кДж/кг
Часть V . Электричество и магнетизм
Электрический ток (сила электрического тока)	A; A (ампер)
Электрический заряд (количество электричества)	С; Кл (кулон)
Пространственная плотность электрического заряда	С/ m 3 ; Кл/м 3	C / mm 3 ; Кл/мм 3 МС/ m 3 ; МКл/м 3 С/с m 3 ; Кл/см 3 kC / m 3 ; кКл/м 3 m С/ m 3 ; мКл/м 3 m С/ m 3 ; мкКл/м 3
Поверхностная плотность электрического заряда	С/ m 2 , Кл/м 2	МС/ m 2 ; МКл/м 2 С/ mm 2 ; Кл/мм 2 С/с m 2 ; Кл/см 2 kC / m 2 ; кКл/м 2 m С/ m 2 ; мКл/м 2 m С/ m 2 ; мкКл/м 2
Напряженность электрического поля		MV / m ; МВ/м kV / m ; кВ/м V / mm ; В/мм V / cm ; В/см mV / m ; мВ/м m V / m ; мкВ/м
Электрическое напряжение, электрический потенциал, разность электрических потенциалов, электродвижущая сила	V , В (вольт)
Электрическое смещение	С/ m 2 ; Кл/м 2	С/с m 2 ; Кл/см 2 kC / cm 2 ; кКл/см 2 m С/ m 2 ; мКл/м 2 m С/ m 2 , мкКл/м 2
Поток электрического смещения
Электрическая емкость	F , Ф (фарад)
Абсолютная диэлектрическая проницаемость, электрическая постоянная		m F / m , мкФ/м nF / m , нФ/м pF / m , пФ/м
Поляризованность	С/ m 2 , Кл/м 2	С/с m 2 , Кл/см 2 kC / m 2 ; кКл/м 2 m С/ m 2 , мКл/м 2 m С/ m 2 ; мкКл/м 2
Электрический момент диполя	С × m , Кл × м
Плотность электрического тока	А/ m 2 , А/м 2	МА/ m 2 , МА/м 2 А/ mm 2 , А/мм 2 A /с m 2 , А/см 2 kA / m 2 , кА/м 2 ,
Линейная плотность электрического тока		kA / m ; кА/м А/ mm ; А/мм А/с m ; А/см
Напряженность магнитного поля		kA / m ; кА/м A / mm ; А/мм A / cm ; А/см
Магнитодвижущая сила, разность магнитных потенциалов
Магнитная индукция, плотность магнитного потока	Т; Тл (тесла)
Магнитный поток	Wb , Вб (вебер)
Магнитный векторный потенциал	Т × m ; Тл × м	kT × m ; кТл × м
Индуктивность, взаимная индуктивность	Н; Гн (генри)
Абсолютная магнитная проницаемость, магнитная постоянная		m Н/ m ; мкГн/м nH / m ; нГн/м
Магнитный момент	А × m 2 ; А м 2
Намагниченность		kA / m ; кА/м А/ mm ; А/мм
Магнитная поляризация
Электрическое сопротивление
Электрическая проводимость	S ; См (сименс)
Удельное электрическое сопротивление	W × m ; Ом × м	G W × m ; ГОм × м М W × m ; МОм × м k W × m ; кОм × м W × cm ; Ом × см m W × m ; мОм × м m W × m ; мкОм × м n W × m ; нОм × м
Удельная электрическая проводимость		MS / m ; МСм/м kS / m ; кСм/м
Магнитное сопротивление
Магнитная проводимость
Полное сопротивление
Модуль полного сопротивления
Реактивное сопротивление
Активное сопротивление
Полная проводимость
Модуль полной проводимости
Реактивная проводимость
Активная проводимость
Активная мощность
Реактивная мощность
Полная мощность			V × A , В × А
Часть VI . Свет и связанные с ним электромагнитные излучения
Длина волны
Волновое число
Энергия излучения
Поток излучения, мощность излучения
Энергетическая сила света (сила излучения)	W / sr ; Вт/ср
Энергетическая яркость (лучистость)	W /(sr × m 2); Вт/(ср × м 2)
Энергетическая освещенность (облученность)	W / m 2 ; Вт/м 2
Энергетическая светимость (нзлучательность)	W / m 2 ; Вт/м 2
Сила света
Световой поток	lm ; лм (люмен)
Световая энергия	lm × s ; лм × с		lm × h; лм × ч
Яркость	cd / m 2 ; кд/м 2
Светимость	lm / m 2 ; лм/м 2
Освещенность	l х; лк (люкс)
Световая экспозиция	lx × s ; лк × с
Световой эквивалент потока излучения	lm / W ; лм/Вт
Часть VII . Акустика
Период
Частота периодического процесса
Длина волны
Звуковое давление		m Ра; мкПа
Скорость колебания частицы		mm / s ; мм/с
Объемная скорость	m 3 / s ; м 3 /с
Скорость звука
Поток звуковой энергии, звуковая мощность
Интенсивность звука	W / m 2 ; Вт/м 2	mW / m 2 ; мВт/м 2 m W / m 2 ; мкВт/м 2 pW / m 2 ; пВт/м 2
Удельное акустическое сопротивление	Pa × s / m ; Па × с/м
Акустическое сопротивление	Pa × s / m 3 ; Па × с/м 3
Механическое сопротивление	N × s / m ; Н × с/м
Эквивалентная площадь поглощения поверхностью или предметом
Время реверберации
Часть VIII Физическая химия и молекулярная физика
Количество вещества	mol ; моль (моль)	kmol ; кмоль mmol ; ммоль m mol ; мкмоль
Молярная масса	kg / mol ; кг/моль	g / mol ; г/моль
Молярный объем	m 3 / moi ; м 3 /моль	dm 3 / mol ; дм 3 /моль cm 3 / mol ; см 3 /моль	l / mol ; л/моль
Молярная внутренняя энергия	J / mol ; Дж/моль	kJ / mol ; кДж/моль
Молярная энтальпия	J / mol ; Дж/моль	kJ / mol ; кДж/моль
Химический потенциал	J / mol ; Дж/моль	kJ / mol ; кДж/моль
Химическое сродство	J / mol ; Дж/моль	kJ / mol ; кДж/моль
Молярная теплоемкость	J /(mol × K); Дж/(моль × К)
Молярная энтропия	J /(mol × K); Дж/(моль × К)
Молярная концентрация	mol / m 3 ; моль/м 3	kmol / m 3 ; кмоль/м 3 mol / dm 3 ; моль/дм 3	mol /1; моль/л
Удельная адсорбция	mol / kg ; моль/кг	mmol / kg ; ммоль/кг
Температуропроводность	M 2 / s ; м 2 /с
Часть IX . Ионизирующие излучения
Поглощенная доза излучения, керма, показатель поглощенной дозы (поглощенная доза ионизирующего излучения)	Gy ; Гр (грэй)	m G у; мкГр
Активность нуклида в радиоактивном источнике (активность радионуклида)	Bq ; Бк (беккерель)

(Измененная редакция,
Изм. № 3).

Таблица 2

Наименование логарифмической величины	Обозначение единицы	Исходное значение величины
Уровень звукового давления
Уровень звуковой мощности
Уровень интенсивности звука
Разность уровней мощности
Усиление, ослабление
Коэффициент затухания

Справочное

1. Разделы 1 — 3
(пп. 3.1 и 3.2); 4, 5 и обязательное Приложение 1 к ГОСТ 8.417-81 соответствуют разделам 1 — 5
и приложению к СТ СЭВ 1052-78. 2. Справочное
приложение 3 к ГОСТ 8.417-81
соответствует информационному приложению к СТ СЭВ 1052-78.

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях — мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

постоянная Авогадро;

увеличение оптического прибора;

концентрация вещества;

число Дебая;

полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

показатель преломления, причем он может быть абсолютным или относительным;

нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

Еще одна формула с N в физике —
частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:

Появляется буква «эн» в формуле для периода обращения:

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n 21 = v 1: v 2 = n 2: n 1 ,

где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1.
Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ.
Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул.
Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение.
Вычислим сначала работу, а потом — мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.

Ответ.
Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2.
Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с: v.

Решение.
Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ.
Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3.
Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи.
Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.

Решение.
В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ.
Значение угла преломления — 26º.

Задачи на период обращения

№4.
Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул
. Период вращения и число оборотов связаны формулой Т = t: N.

Решение.
Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.

Ответ.
Число оборотов лопастей мельницы равно 720.

№5.
Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула
: частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение.
В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ.
Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n
или
N, ему нужно
разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.

Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.

Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.

Величины

Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.

Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.

Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три — добавляется еще и высота.

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».

Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.

Длина

Как уже было указано, в математике длина, высота, ширина — это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.

В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.

Высота

Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.

На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина — все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и строчная или заглавная «R»/«r».

Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением — диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.

Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение — большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга — «Ø».

Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».

Толщина

Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр — толщина.

Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так — нет информации.

Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь — это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.

GISMETEO: Что значат миллиметры осадков в прогнозе? 20 мм — это много или мало? — Климат

Атмосферные осадки — это вода в жидком и твердом состоянии, выпадающая из облаков, или осаждающаяся непосредственно из воздуха. Среди осадков, выпадающих из облаков, наиболее распространены: дождь, морось, снег, мокрый снег, снежная крупа, ледяная крупа, снежные зерна, град, ледяной дождь, ледяные иглы. Непосредственно из воздуха осаждаются: роса, иней, изморозь. Осаждение переохлажденных: дождя, мороси и тумана, на земле и предметах дает гололед.

shutterstock.com

Каждый из этих видов осадков приносит какое-то количество влаги. Для того чтобы оценить, сколько выпадет, или выпало влаги, применяется понятие «количество осадков».

Количество осадков — это высота слоя воды в миллиметрах, который образовался бы на поверхности земли, если бы она была абсолютно ровная, то есть осадки бы не стекали, не просачивались в почву и не испарялись.

Иногда при интенсивных дождях можно видеть, как улицы превращаются в «реки», но при этом метеорологи говорят, что выпало «всего» 15 мм осадков.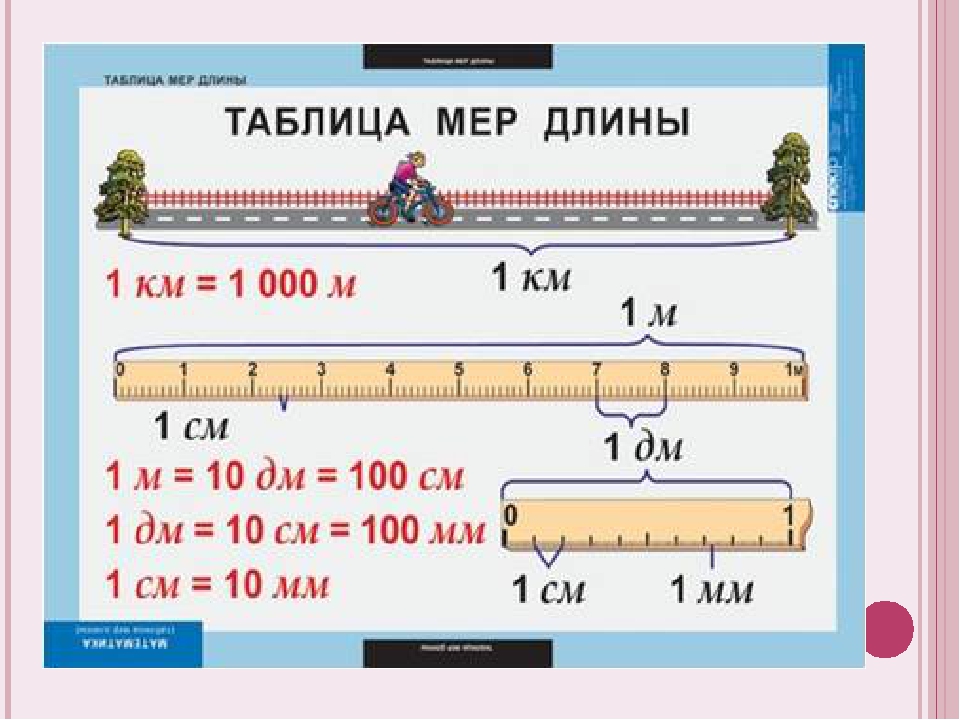 Количество осадков в миллиметрах численно равно массе воды, выпавшей на горизонтальную площадку в 1 квадратный метр

15 мм осадков — это 15 килограммов воды на каждый квадратный метр земной поверхности. Это не такое уж маленькое количество — полтора ведра! С учетом того, что земная поверхность неровная, то выпавшие осадки стекают в пониженные участки, образуя бурные ручьи и глубокие лужи.

Гисметео

В случае со снегом следует разделять понятия «количество осадков» и «высота снежного покрова». Как известно, снег бывает разным — сухим, мокрым, мелким, крупным. В зависимости от вертикального профиля температуры и влажности снежинки имеют различную структуру. При низкой температуре и слабом ветре крупные снежинки нагромождаются друг на друга, образуя небольшой по плотности, но большой по высоте снежный покров. И наоборот — при сильном ветре и мелком снеге снежный покров получается плотным и невысоким.

Как в таких случаях понять, какое количество влаги выпало в первом случае и во втором? Для этого снег растапливают и получают миллиметры воды. Это важно знать не только для сравнения двух снегопадов, но для оценки влагонакопления за месяц или сезон, для того, чтобы оценить, сколько влаги почва получит весной, и т. д.

Высота снежного покрова имеет некоторую корреляцию с количеством выпавших осадков. В зависимости от структуры, 1 мм выпавшего снега в жидком эквиваленте может соответствовать 1–1,5 см снежного покрова.

Какая водостойкость палатки вам подойдет? / Палатки / Статьи

Одной из главных эксплуатационных характеристик палатки является ее водостойкость. Палатка используется не только при благоприятных погодных условиях, но и должна защищать человека от дождя, а так же изолировать от влажной поверхности, на которую может быть установлена.

Водостойкость выражается как высота водяного столба в миллиметрах, который выдерживает внешний тент и пол, при котором ткань еще не пропускает воду и, следовательно, не промокает под давлением дождя и ветра. Для определения степени водостойкости материала в мировой практике используются данные так называемого «гидростатического теста» (JIS 1092 метод A; тест AATCC метод 127). В соответствии с ним образцы ткани стирают 10 раз, чтобы приблизить их к реальным условиям эксплуатации. Затем на площади в 1 см² с помощью специального аппарата создают давление эквивалентное давлению водяного столба определённой высоты, которая измеряется в миллиметрах. 

Сложно понять, что же на самом деле обозначает величина в 1000 или 3000 мм водяного столба.

У классических однослойных палаток линейки Trek Planet водостойкость определяется показателем 1000 мм для внешнего тента и 10000 мм для пола. Такие палатки защитят вас в условиях непродолжительных или моросящих дождей. Быстросборные и классические палатки подойдут для непродолжительного отдыха на природе в выходные или для музыкальных фестивалей.

Для непродолжительных походов и спокойного летнего отдыха на природе отлично подойдут походные палатки Trek Planet c водостойкостью внешнего тента 2000 мм и пола – 10000 мм. Такие показатели водостойкости обеспечат сухую внутреннюю палатку даже во время сильных, но непродолжительных осадков.  

Для многодневных кемпинговых стоянок и продолжительных туристических походов лучше всего подойдет трекинговая палатка или кемпинговая палатка с указанием водостойкости внешнего тента 3000 мм, пола 6000/10000 мм. Такая палатка отлично ведет себя даже в сильный или продолжительный дождь.

Водонепроницаемость дна палатки должна быть всегда выше показателей внешнего тента, потому что находясь в палатке вы обеспечиваете дополнительные зоны давления на материал за счет собственного веса. С показателем от 6000 до 10000 мм дно не промокнет даже во время продолжительных дождей и на влажном грунте.

Помимо водостойкости самих материалов палатки, немаловажно, чтобы все швы на внешней палатке были проклеены. У палаток Trek Planet все швы заклеиваются сразу после пошива палатки специальной лентой путем горячего наплавления, что обеспечивает долговечность и надежную защиту от протечек.

Обратите внимание, что устанавливать палатку надо правильно, особенно в плохую погоду! Тент палатки должен быть максимально натянут и растянут с помощью растяжек, на ткани не должно быть складок, внешняя палатка не должна соприкасаться с внутренней. Если вы ожидаете длительную непогоду, обязательно выберите ровное место на возвышении, чтобы вода не скапливалась под дном палатки, можно даже окопать палатку по периметру. 

Как перевести квадратные метры в квадратные сантиметры или квадратные дециметры

• Альфашкола
• Статьи
• Как перевести квадратные метры в квадратные сантиметры или квадратные дециметры

Для того чтобы правильно перевести квадратные метры в квадратные сантиметры надо вспомнить сколько сантиметов в одном метре: 

(1) м (=) (100) см 

Но у нас квадратные сантиметры поэтому (100*100=10;000), то есть в одном квадратном метре (10;000) квадратных сантиметров. 2).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Харьковский государственный университет им. А.М. Горького

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-11 классов. Имею высшую квалификационную категорию и педагогическое звание «Учитель — методист». В работе использую технологии развивающего, личностно-ориентированного обучения, успешно готовлю выпускников к итоговому независимому оцениванию. Я с детства люблю решать задачи. Мне кажется, что любой человек, который делает открытие, испытывает такое сильное чувство, которое хочется повторить. Любая задача, особенно трудная, позволяет испытать это чувство. Люди, которые увлекаются математикой более успешные в жизни. Ведь вся наша жизнь — это решение задач.
Оставить заявку

Репетитор по математике

Витебский государственный педагогический институт им. С.М. Кирова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-8 классов. На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях!
Оставить заявку

Репетитор по математике

Белорусский государственный педагогический университет им. Максима Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 3-8 классов. Я люблю математику, потому что нахожу ее очень увлекательной. В преподавании придерживаюсь гуманистического и личностно-ориентированного методов обучения. Всегда стараюсь найти общий язык с учеником, стать для него товарищем и поддержкой в процессе обучения. Я гарантирую позитивное и познавательное погружение в увлекательный мир математики!

Логарифмы (урок)

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Курсы ОГЭ

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Функция

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Похожие статьи

Урок 7.

метр. таблица единиц длины — Математика — 2 класс

Математика, 2 класс

Урок №7. Метр. Таблица единиц длины

Перечень вопросов, рассматриваемых в теме:

— Что такое метр?

— Как переводить одни единицы длины в другие: мелкие в более крупные и крупные в более мелкие, используя соотношения между ними?

Глоссарий по теме:

Метр, дециметр, сантиметр, миллиметр — единицы измерения длины.

Таблица мер длины:

1 см = 10 мм

1 дм = 10 см

1 м = 10 дм

1 м = 100 см

Именованные числа — это числа, полученные при измерении величин и сопровождающиеся названием единицы измерения (например: 5 см, 8 м).

Основная и дополнительная литература по теме урока:

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.13

2. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова А. Д. -М.: Просвещение, 2017, с.17, 18

3. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю. И., Волкова А. Д. -М.: Просвещение, Учлит, 2017, с.7, 8

Теоретический материал для самостоятельного изучения

Для измерения длин больших предметов существует более крупная единица измерения – метр.

Сокращенно обозначаем буквой эм — М.

Метр появился на свет в конце восемнадцатого века во Франции.

В жизненной практике мы можем наблюдать, прежде всего, измерение именно с помощью метра. Зайдем в магазин и понаблюдаем, с помощью чего измеряет продавец длину ткани, клеенки, ленты? Конечно же, с помощью метра. Когда ваши родители соберутся делать ремонт, они сначала с помощью метра измерят длину, ширину, высоту комнат, чтобы рассчитать количество обоев, краски. Из этого следует, что метр – основная единица длины.

Посмотрим на рисунок. Сколько сантиметров помещается в данной линейке?

Сто сантиметров. Значит в одном метре сто сантиметров. 1м=100см

Посмотрим на линейку. Подумаем, сколько дециметров в одном метре?

Мы видим, что 1м это 10 дм

Как соотносятся между собой все единицы измерения длины?

Существует таблица мер длины, которую нужно выучить

1 см = 10 мм

1 дм = 10 см

1 м = 10 дм

1 м = 100 см

Именованные числа можно преобразовывать — сантиметры переводить в миллиметры, дециметры переводить в сантиметры и наоборот.

Например: пять дециметров семь сантиметров нужно перевести в сантиметры

Пять дециметров — это пятьдесят сантиметров, да еще семь сантиметров равно пятьдесят семь сантиметров.

Запишем это так: 5 дм 7 см = ? см

5 дм 7 см = 50 см + 7 см = 57 см

Семьдесят пять сантиметров переведем в дециметры и сантиметры. Семьдесят пять сантиметров — это семьдесят сантиметров и пять сантиметров. Семьдесят сантиметров — это семь дециметров. Получается: семьдесят пять сантиметров — это семь дециметров и пять сантиметров.

Запишем это так: 75 см = ?дм ? см

75 см = 70 см + 5 см = 7 дм 5 см

Сравним два именованных числа: 1 м и 5 дм.

Удобнее сравнивать одинаковые единицы длины, поэтому один метр переведем в дециметры.

В 1 м — 10 дм.

10 дм> 5 дм, значит,

1 м > 5 дм

10 дм> 5 дм

Тренировочные задания.

1. Сравните именованные числа.

4 дм * 4 см 2 мм 61см * 90 мм

5 м * 70 дм 3 см 3 мм * 33 мм

Правильные ответы:

4 дм> 4 см 2 мм 61 см > 90 мм

5 м < 70дм 3 см 3 мм = 33 мм

2. Догадайтесь, какие единицы длины пропущены, запишите их

Высота парты — 65____

Рост Дюймовочки — 25___

Высота треэтажного дома — 11____

Рост ученика — 1___40___

Правильные ответы:

Высота парты — 65 СМ

Рост Дюймовочки — 25 ММ

Высота трехэтажного дома — 11 М

Рост ученика — 1 М 40 СМ

Внутренний объем погонного метра трубы в литрах — таблица.

Внутренний диаметр трубы 4-1000 мм. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения трубопровода.

Внутренний объем погонного метра трубы в литрах — таблица. Внутренний диаметр трубы 4-1000 мм. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения трубопровода. Пустяк, а времени такая табличка много экономит. Внутренний диаметр,мм Внутренний объем 1 м погонного трубы, литров Внутренний объем 10 м погонных трубы, литров Внутренний диаметр,мм Внутренний объем 1 м погонного трубы, литров Внутренний объем 10 м погонных трубы, литров 4 0,0126 0,1257 105 8,6590 86,5901 5 0,0196 0,1963 110 9,5033 95,0332 6 0,0283 0,2827 115 10,3869 103,8689 7 0,0385 0,3848 120 11,3097 113,0973 8 0,0503 0,5027 125 12,2718 122,7185 9 0,0636 0,6362 130 13,2732 132,7323 10 0,0785 0,7854 135 14,3139 143,1388 11 0,0950 0,9503 140 15,3938 153,9380 12 0,1131 1,1310 145 16,5130 165,1300 13 0,1327 1,3273 150 17,6715 176,7146 14 0,1539 1,5394 160 20,1062 201,0619 15 0,1767 1,7671 170 22,6980 226,9801 16 0,2011 2,0106 180 25,4469 254,4690 17 0,2270 2,2698 190 28,3529 283,5287 18 0,2545 2,5447 200 31,4159 314,1593 19 0,2835 2,8353 210 34,6361 346,3606 20 0,3142 3,1416 220 38,0133 380,1327 21 0,3464 3,4636 230 41,5476 415,4756 22 0,3801 3,8013 240 45,2389 452,3893 23 0,4155 4,1548 250 49,0874 490,8739 24 0,4524 4,5239 260 53,0929 530,9292 26 0,5309 5,3093 270 57,2555 572,5553 28 0,6158 6,1575 280 61,5752 615,7522 30 0,7069 7,0686 290 66,0520 660,5199 32 0,8042 8,0425 300 70,6858 706,8583 34 0,9079 9,0792 320 80,4248 804,2477 36 1,0179 10,1788 340 90,7920 907,9203 38 1,1341 11,3411 360 101,7876 1017,8760 40 1,2566 12,5664 380 113,4115 1134,1149 42 1,3854 13,8544 400 125,6637 1256,6371 44 1,5205 15,2053 420 138,5442 1385,4424 46 1,6619 16,6190 440 152,0531 1520,5308 48 1,8096 18,0956 460 166,1903 1661,9025 50 1,9635 19,6350 480 180,9557 1809,5574 52 2,1237 21,2372 500 196,3495 1963,4954 54 2,2902 22,9022 520 212,3717 2123,7166 56 2,4630 24,6301 540 229,0221 2290,2210 58 2,6421 26,4208 560 246,3009 2463,0086 60 2,8274 28,2743 580 264,2079 2642,0794 62 3,0191 30,1907 600 282,7433 2827,4334 64 3,2170 32,1699 620 301,9071 3019,0705 66 3,4212 34,2119 640 321,6991 3216,9909 68 3,6317 36,3168 660 342,1194 3421,1944 70 3,8485 38,4845 680 363,1681 3631,6811 72 4,0715 40,7150 700 384,8451 3848,4510 74 4,3008 43,0084 720 407,1504 4071,5041 76 4,5365 45,3646 740 430,0840 4300,8403 78 4,7784 47,7836 760 453,6460 4536,4598 80 5,0265 50,2655 780 477,8362 4778,3624 82 5,2810 52,8102 800 502,6548 5026,5482 84 5,5418 55,4177 820 528,1017 5281,0173 86 5,8088 58,0880 840 554,1769 5541,7694 88 6,0821 60,8212 860 580,8805 5808,8048 90 6,3617 63,6173 880 608,2123 6082,1234 92 6,6476 66,4761 900 636,1725 6361,7251 94 6,9398 69,3978 920 664,7610 6647,6101 96 7,2382 72,3823 940 693,9778 6939,7782 98 7,5430 75,4296 960 723,8229 7238,2295 100 7,8540 78,5398 980 754,2964 7542,9640 — — — 1000 785,3982 7853,9816

Внутренний объем погонного метра трубы в литрах — таблица.

Внутренний диаметр трубы 4-1000 мм. Масса воды в трубе. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения

Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг 4 0,0126 0,1257 105 8,6590 86,5901 5 0,0196 0,1963 110 9,5033 95,0332 6 0,0283 0,2827 115 10,3869 103,8689 7 0,0385 0,3848 120 11,3097 113,0973 8 0,0503 0,5027 125 12,2718 122,7185 9 0,0636 0,6362 130 13,2732 132,7323 10 0,0785 0,7854 135 14,3139 143,1388 11 0,0950 0,9503 140 15,3938 153,9380 12 0,1131 1,1310 145 16,5130 165,1300 13 0,1327 1,3273 150 17,6715 176,7146 14 0,1539 1,5394 160 20,1062 201,0619 15 0,1767 1,7671 170 22,6980 226,9801 16 0,2011 2,0106 180 25,4469 254,4690 17 0,2270 2,2698 190 28,3529 283,5287 18 0,2545 2,5447 200 31,4159 314,1593 19 0,2835 2,8353 210 34,6361 346,3606 20 0,3142 3,1416 220 38,0133 380,1327 21 0,3464 3,4636 230 41,5476 415,4756 22 0,3801 3,8013 240 45,2389 452,3893 23 0,4155 4,1548 250 49,0874 490,8739 24 0,4524 4,5239 260 53,0929 530,9292 26 0,5309 5,3093 270 57,2555 572,5553 28 0,6158 6,1575 280 61,5752 615,7522 30 0,7069 7,0686 290 66,0520 660,5199 32 0,8042 8,0425 300 70,6858 706,8583 34 0,9079 9,0792 320 80,4248 804,2477 36 1,0179 10,1788 340 90,7920 907,9203 38 1,1341 11,3411 360 101,7876 1017,8760 40 1,2566 12,5664 380 113,4115 1134,1149 42 1,3854 13,8544 400 125,6637 1256,6371 44 1,5205 15,2053 420 138,5442 1385,4424 46 1,6619 16,6190 440 152,0531 1520,5308 48 1,8096 18,0956 460 166,1903 1661,9025 50 1,9635 19,6350 480 180,9557 1809,5574 Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг 52 2,1237 21,2372 500 196,3495 1963,4954 54 2,2902 22,9022 520 212,3717 2123,7166 56 2,4630 24,6301 540 229,0221 2290,2210 58 2,6421 26,4208 560 246,3009 2463,0086 60 2,8274 28,2743 580 264,2079 2642,0794 62 3,0191 30,1907 600 282,7433 2827,4334 64 3,2170 32,1699 620 301,9071 3019,0705 66 3,4212 34,2119 640 321,6991 3216,9909 68 3,6317 36,3168 660 342,1194 3421,1944 70 3,8485 38,4845 680 363,1681 3631,6811 72 4,0715 40,7150 700 384,8451 3848,4510 74 4,3008 43,0084 720 407,1504 4071,5041 76 4,5365 45,3646 740 430,0840 4300,8403 78 4,7784 47,7836 760 453,6460 4536,4598 80 5,0265 50,2655 780 477,8362 4778,3624 82 5,2810 52,8102 800 502,6548 5026,5482 84 5,5418 55,4177 820 528,1017 5281,0173 86 5,8088 58,0880 840 554,1769 5541,7694 88 6,0821 60,8212 860 580,8805 5808,8048 90 6,3617 63,6173 880 608,2123 6082,1234 92 6,6476 66,4761 900 636,1725 6361,7251 94 6,9398 69,3978 920 664,7610 6647,6101 96 7,2382 72,3823 940 693,9778 6939,7782 98 7,5430 75,4296 960 723,8229 7238,2295 100 7,8540 78,5398 980 754,2964 7542,9640 — — — 1000 785,3982 7853,9816 Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг Внутренний диаметр, мм Объем внутр. 1 м трубы, литров = масса воды в 1 м, кг Объем внутр. 10 м трубы, литров = масса воды в 10 м, кг

Как найти Масштаб в Математике?

Понятие масштаба

Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.

Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.

Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.

• Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.

Масштаб бывает трех видов:

• численный, выражается в числах 1:1000;
• именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
• линейный, зная величину масштаба, можно определить расстояния.

Определение масштаба на карте

На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.

Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.

Масштаб — это отношение размера изображения к размеру изображаемого объекта.

Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.

На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.

Численные масштабы карт и соответствующие им масштабы на местности:

Масштаб 1 : 100 000

• 1 мм на карте — 100 м (0,1 км) на местности
• 1 см на карте — 1000 м (1 км) на местности
• 10 см на карте — 10000 м (10 км) на местности

Масштаб 1 : 10000

• 1 мм на карте — 10 м (0,01 км) на местности
• 1 см на карте — 100 м (0,1 км) на местности
• 10 см на карте — 1000 м (1 км) на местности

Масштаб 1 : 5000

• 1 мм на карте — 5 м (0,005 км) на местности
• 1 см на карте — 50 м (0,05 км) на местности
• 10 см на карте — 500 м (0,5 км) на местности

Масштаб 1 : 2000

• 1 мм на карте — 2 м (0,002 км) на местности
• 1 см на карте — 20 м (0,02 км) на местности
• 10 см на карте — 200 м (0,2 км) на местности

Масштаб 1 : 1000

• 1 мм на карте — 100 см (1 м) на местности
• 1 см на карте — 1000 см (10 м) на местности
• 10 см на карте — 100 м на местности

Масштаб 1 : 500

• 1 мм на карте — 50 см (0,5 метра) на местности
• 1 см на карте — 5 м на местности
• 10 см на карте — 50 м на местности

Масштаб 1 : 200

• 1 мм на карте — 0,2 м (20 см) на местности
• 1 см на карте — 2 м (200 см) на местности
• 10 см на карте — 20 м (0,2 км) на местности

Масштаб 1 : 100

• 1 мм на карте — 0,1 м (10 см) на местности
• 1 см на карте — 1 м (100 см) на местности
• 10 см на карте — 10м (0,01 км) на местности

Решение задач на масштаб

Для закрепления темы решим несколько математических задач на масштаб за 6 класс.

Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.

Как решаем:

8 см — это 1 часть

8 * 10 000 = 80 000 (см) — это 10 000 частей

80 000 см = 800 м

Ответ: 800 м

Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.

Как решаем:

400 км = 400 000 м = 40 000 000 см

40000000 : 5000000 = 40 : 5 = 8

Ответ: 8 см

Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?

Как решаем:

700 км = 700 000 м = 70 000 000 см

70 000 000 : 14 = 5 000 000

Ответ: уменьшить в 5 000 000 раз.

Преобразование 1000 мм в дюймы

››
Перевести миллиметры в дюймы

Пожалуйста, включите Javascript для использования
конвертер величин.
Обратите внимание, что вы можете отключить большинство объявлений здесь:
https://www.convertunits.com/contact/remove-some-ads.php

››
Дополнительная информация в конвертере величин

Сколько миллиметров в 1 дюйме?
Ответ 25,4.
Мы предполагаем, что вы конвертируете между миллиметрами и дюймами .
Вы можете просмотреть более подробную информацию о каждой единице измерения:
мм или
дюймы
Базовая единица СИ для длины — метр.
1 метр равен 1000 мм, или 39,370078740157 дюймов.
Обратите внимание, что могут возникать ошибки округления, поэтому всегда проверяйте результаты.
Используйте эту страницу, чтобы узнать, как преобразовать миллиметры в дюймы.
Введите свои числа в форму для преобразования единиц!

››
Таблица быстрого перевода миллиметров в дюймы

1 мм в дюймах = 0,03937 дюйма

10 дюймов в дюймы = 0,3937 дюйма

20 дюймов в дюймы = 0,7874 дюйма

30 дюймов в дюймы = 1. 1811 дюймов

40 мм в дюймах = 1,5748 дюймов

50 мм в дюймах = 1,9685 дюймов

100 мм в дюймах = 3,93701 дюймов

200 дюймов в дюймы = 7,87 402 дюймов

››
Хотите другие юниты?

Вы можете произвести обратное преобразование единиц измерения из
дюймы в мм или введите любые две единицы ниже:

››
Обычные преобразования длины

мм до военного темпа
мм до калибра
мм до линии
мм до морской мили
мм до квадранта
мм до стадиона
мм до канны
мм до аршина
мм до пчелиного пространства
мм до мыса

››
Определение: миллиметр

Миллиметр (американское написание: миллиметр, символ мм) — одна тысячная метра, которая является базовой единицей длины Международной системы единиц (СИ).Миллиметр — это часть метрической системы. Соответствующей единицей площади является квадратный миллиметр, а соответствующей единицей объема — кубический миллиметр.

››
Определение: дюйм

Дюйм — это название единицы длины в различных системах, включая имперские единицы и общепринятые единицы измерения США. В ярде 36 дюймов, а в футе — 12 дюймов. Дюйм обычно является универсальной единицей измерения в Соединенных Штатах и ​​широко используется в Великобритании и Канаде, несмотря на введение метрики в последние две единицы в 1960-х и 1970-х годах соответственно.Дюйм все еще широко используется неформально, хотя и несколько реже, в других странах Содружества, таких как Австралия; Примером может служить давняя традиция измерять рост новорожденных детей в дюймах, а не в сантиметрах. Международный дюйм равен 25,4 миллиметрам.

››
Метрические преобразования и др.

ConvertUnits.com предоставляет онлайн
калькулятор преобразования для всех типов единиц измерения.
Вы также можете найти метрические таблицы преобразования для единиц СИ.
в виде английских единиц, валюты и других данных.Введите единицу
символы, сокращения или полные названия единиц длины,
площадь, масса, давление и другие типы. Примеры включают мм,
дюйм, 100 кг, жидкая унция США, 6 футов 3 дюйма, 10 стоун 4, кубический см,
метры в квадрате, граммы, моль, футы в секунду и многое другое!

1000 MM в дюймов — Howmanypedia.com

Добро пожаловать на нашу страницу, где показано, как преобразовать 1000 мм в дюймы. Есть много случаев, когда вам нужно выполнить это преобразование. Некоторые продукты рекламируются в миллиметрах (мм), но что, если вы знакомы только с их дюймовым эквивалентом? На этой странице мы покажем вам эквивалент 1000 мм в дюймах.Мы также показываем множество методов преобразования.

Калькулятор 1000 дюймов в MM

1000 мм равно 39,3701 дюйм. Для расчета воспользуйтесь нашим онлайн-калькулятором.

В поле рядом с «миллиметрами» введите 1000. После ввода числа калькулятор отобразит результаты. Запомнив числа, нажмите кнопку сброса, если хотите выполнить другие преобразования.

Мы использовали 1000 мм в качестве примера, потому что это основное внимание на этой странице.Однако вы можете использовать тот же метод для других значений в миллиметрах. Например, если вы хотите преобразовать 20 мм, просто введите 20 в поле миллиметра.

Сокращения в дюймах: дюймов, “.

Аббревиатура в миллиметрах: «мм».

1000 MM в дюймов — Определение единиц

Миллиметры Определение — Миллиметр — это единица измерения малых объектов. Он относится к метрической системе и эквивалентен 0,001 метру. Он сокращенно обозначается как мм.Написание «миллиметр» используется в Соединенных Штатах, но в Великобритании и других странах оно пишется как миллиметр.

Миллиметр примерно равен 0,04 дюйма (точнее, 0,0393700787402 дюйма). Мм меньше сантиметра, так как 1 мм равен 0,1 сантиметра в метрической системе. 1000 миллиметров эквивалентны 1000 мм, а миллиметры используются, когда объект слишком мал для дюймов.

Дюймы Определение — Для американцев дюйм является предпочтительной единицей измерения.Это равно 1/36 ярда. 12 дюймов эквивалентны футу. Дюйм происходит от слова ynce или ince, которое происходит от uncia. У дюйма есть два сокращения: дюйм и “. Помимо США, Канада и Великобритания используют это для измерения. В Японии дюйм используется для измерения экранов дисплеев.

Официальный символ дюйма — дюйм, но в большинстве случаев он отображается как двойной штрих («), тот же символ, что используется для кавычек, например, 5».

1000 Мм в дюймы Таблица преобразования

Калькулятор из миллиметров в дюймы — это хорошо, но если вам нужно сразу выполнить серию преобразований, подойдет эта таблица преобразования.Например, вы можете использовать его для расчета эквивалента 1000 мм в дюймах. Если вам нужно быстро сравнить, используйте это, потому что это быстро и легко.

Преобразование единиц	Миллиметры (мм)	дюймов (дюймов)
1000 дюймов в миллиметр	1000 мм =	39,3701 ”

1000 дюймов в миллиметр

Если вы хотите преобразовать 1000 мм в дюймы, используйте ту же технику для преобразования стандартных миллиметров в дюймы.

Все, что вам нужно сделать, это разделить 1000 на 25,4. Имейте в виду, что 1 дюйм эквивалентен 25,4 мм. Отсюда следует, что вам просто нужно разделить 1000 мм, используя это число. Используя эту формулу, мы получаем 39,3701 дюйм.

Результаты можно записать следующими способами:

• 1000 мм = 39,3701 дюйм
• 1000 мм = 39,3701 ”
• 1000 мм = 39,3701 дюйм
• 1000 миллиметров = 39,3701 дюйма

Перевести 1000 мм в дюймы не так уж и сложно.Если у вас есть конвертер или калькулятор, процесс прост. Как мы уже указывали, будет много случаев, когда вам придется выполнить это преобразование, поэтому знание процесса поможет.

Неважно, покупаете ли вы или делаете что-то, осведомленность о конверсии избавит вас от неприятностей.

преобразовать 1000 мм в дюймы

Если вы занимаетесь строительством или много путешествуете, вы обнаружите, что используются либо миллиметры, либо дюймы. Если вы знакомы только с дюймами, вам понадобятся знания.Например, вы можете найти устройство толщиной 1000 мм. Теперь вам интересно, сколько это в дюймах?

Если вы привыкли к дюйму, трудно представить себе, что такое 1000 мм. Вот почему вам понадобится диаграмма или калькулятор для преобразования. Если вы знаете, как преобразовать 1000 мм в дюймы, вы можете использовать ту же процедуру для 20 мм, 30 мм и так далее.

Выбор наиболее эффективного метода зависит от вас. Для многих калькулятор — самый эффективный. Не нужно придумывать, какую цифру делить или умножать.Просто введите 1000 мм, и вы получите результат.

Невозможно переоценить важность наличия диаграммы или калькулятора. Возможно, вы знаете, что 1 мм равен 0,04 дюйма. Вы также можете знать, что вы можете разделить 1000 мм на 25,4 и получить эквивалент в дюймах. Но вручную это сделать сложно. Вместо того, чтобы вычислять вручную, наши варианты здесь быстрее.

Популярные преобразования из MM в дюймы (миллиметры в дюймы):

1000 мм равно сколько дюймов?

Чтобы сразу ответить на этот вопрос, 1000 миллиметров эквивалентны 39.3701 дюйм. Многие люди ищут преобразование 1000 мм в дюймы, потому что это измерение широко используется. Если вы знаете, как найти дюйм, эквивалентный 1000 мм, вам будет легче сделать это и с другими измерениями.

Однако для справки у нас есть другие общие значения в миллиметрах, используемые для других измерений.

Когда была создана метрическая система, цель заключалась в том, чтобы сделать ее универсальным средством измерения. Уже тогда специалисты знали, что практичнее будет использовать одни и те же единицы измерения.

Однако этого еще не произошло. Компании и люди в США, Канаде и Великобритании используют дюймы, в то время как другие выбирают миллиметры. В этой ситуации очень важно научиться преобразовывать 1000 мм в дюймы. Это сэкономит вам много времени.

Сводка

Название изделия

1000 мм в дюймах

Описание

На этой странице отображается эквивалент 1000 мм в дюймах. Мы также показываем множество методов преобразования. Мы предлагаем ознакомиться с нашим конвертером 1000 мм в дюймы и таблицей.

Автор

Howmanypedia.com

Имя издателя

Howmanypedia

Логотип издателя

Преобразование 1000 миллиметров в дюймы — Преобразование 1000 миллиметров в дюймы (мм в дюймы)

Преобразование 1000 миллиметров в дюймы

1000 миллиметров в дюймы — Миллиметры в дюймы — Расстояние и длина — Преобразование

Вы переводите единицы измерения расстояния и длины от миллиметров до дюймов

1000 миллиметров (мм)

=

39.37008 дюймов (дюймов)

Визит 1000 дюймов в миллиметры Преобразование

Миллиметры:
Миллиметр (символ СИ мм) — это единица измерения длины в метрической системе, равная 1/1000 метра (или 1E-3 метра), которая также является стандартной инженерной единицей. 1 дюйм = 25,4 мм.

дюймов:
Дюйм (символ: дюйм) — это единица длины. Он определяется как 1⁄12 фута, а также как 1⁄36 ярда. Хотя традиционные стандарты точной длины дюйма менялись, она равна ровно 25.4 мм. Дюйм — это широко используемая единица измерения длины в США, Канаде и Великобритании.

Калькулятор преобразования расстояний и длин ) Двор (ярд) Общие единицы AlnAngstrom (Å) ArpentАстрономическая единица (au) Аттометр (am) Ячменное зерно Калибр (cl) Цепь (ch) Гвоздь из ткани (cn) Ширина ткани (cs) Кубит (библейский) (куб.) Кубит (греческий) ( детеныш.) Дециметр (дм) Декаметр (плотина) Exametre (Em) FamnFathom (ftm) Фемтометр (fm) FermiFingerbreadth (библейский) (fing.) Foot (американский обзор) (ft) Furlong (мех) Gigametre (Gm) HandHandbreadth (библейский) ( handb.) гектометр (hm) KenKiloparsec (kpc) LeagueLight Year (ly) Link (li) Long Cubit (библейский) (lc) Long Reed (библейский) (lr) мегаметр (мм) Megaparsec (Mpc) MicrometerMilMil (Швеция) Mile ( Римская) Миля (фут съемки США) (мили) Нанометр (нм) Парсек (ПК) ОкуньПетаметр (Pm) PicaPicometer (pm) PlanckPointPole (rd) Рид (библейский) Rod (rd) Римский ActusРусский ArchinSpan (библейский) Terameter (TM) TwipVara CastellanaVara ConuqueraVara De Tarea Преобразовать в:

в

Общие единицы Сантиметр (см) Фут (фут) Дюйм (дюйм) Километр (км) Метр (м) Миля (США) (мили) Миллиметр (мм) Морская миля (Нм) Ярд (ярд) Общие единицы AlnAngstrom (Å) ArpentАстрономическая единица (au) Аттометр (am) Ячменное зерно Калибр (cl) Цепь (ch) Тканевый гвоздь (c.n.) Cloth Span (cs) Cubit (библейский) (куб.) Cubit (греческий) (куб.) Дециметр (dm) Декаметр (плотина) Exametre (Em) FamnFathom (ftm) Фемтометр (fm) Fermi Fingerbreadth (библейский) (fing .) Фут (исследование США) (футы) Ферлонг (мех) Гигаметр (Гм) Ширина руки (Библейский) (ручн.) Гектометр (гм) Кенкилопарсек (кпк) Лига Свет Год (ly) Ссылка (li) Длинный кубит (Библейский) (lc ) Длинный тростник (библейский) (lr) Мегаметр (Mm) Megaparsec (Mpc) MicrometerMilMil (Швеция) Миля (Roman) Миля (американский фут) (мили) Нанометр (нм) Парсек (pc) PerchPetameter (Pm) PicaPicometer (pm) PlanckPointPole (rd) Reed (библейский) Rod (rd) Roman ActusРусский ArchinSpan (библейский) Terameter (Tm) TwipVara CastellanaVara ConuqueraVara De Tarea Результат:

Преобразование из футов и дюймов в метры

футов (фут)
+

дюйм (дюйм)
=

Метр (м)

Таблица преобразования длины

9014 9014

	миллиметр (мм)	сантиметр (см)	метр (м)	километр (км)	дюйм (дюйм)	фут / фут (фут)	ярд (ярд)	миля (миль)
1 миллиметр (мм)	1	0.1	0,001	0,000001	0,03937	0,003281	0,0010936	0,0000006214
1 см	0,000006214
1 метр (м)	1000	100	1	0,001	39,37	3,281	1,0936	0.0006214
1 километр (км)	1000000	100000	1000	1	39370	3281	1093,6	0,6214	4	9014 902 901 2,5 дюйма	0,0254	0,0000254	1	0,08333	0,02778	0,000015783
1 фут / фут (фут)	304,8	30,48	0.3048	0,0003048	12	1	0,33333	0,0001894
1 ярд (ярд)	914,4	91,44	0,			01414		01414
1 миля (миль)	1609344	160934	1609,3	1,6093	63360	5280	1760	1					9014							1852	1.852	72913	6076	2025,4	1,1508

Мы решили округлить некоторые коэффициенты пересчета, чтобы они соответствовали этой таблице. Поэтому некоторые из этих значений неточны, но все же имеют разумную точность.

Самые популярные пары преобразования расстояния и длины

• Сантиметр в фут
• Сантиметр в дюйм
• Сантиметр в километр
• Сантиметр в метр
• Сантиметр в милю (США)
• Морской метр в миллиметр
• сантиметр до ярда
• фут до сантиметра
• фут до дюйма
• фут до километра
• фут до метра
• фут до мили (США)
• фут до миллиметра
• фут до морской мили
• фут до морской мили
• дюймы в сантиметры
• дюймы в футы
• дюймы в километры
• дюймы в метры
• дюймы в миллиметры (США)
• дюймы в миллиметры
• дюймы в морские мили
• дюймов в километры

от

• дюймов до ярдов

Километр в фут

• Километр в дюйм
• Километр в метр
• Километр в миля (США )
• Миллиметр в Миллиметр
• Километр в Морская Миля
• Километр в Ярд
• Метр в Сантиметр
• Метр в Фут
• Метр в Дюйм
• Метр в Километр

Миллион

• Метр в Мил
• метров до морских миль
• метров до ярдов
• миль (США) до сантиметров
• миль (США) до футов
• миль (США) до дюймов
• миль (США) до километров
• миль (США) до Метр
• миля (США) — миллиметр
• миля (США) — морская миля
• миля (США) — ярд
• миллиметр — сантиметр
• миллиметр — фут
• миллиметр — дюйм
• миллиметр

миллиметр — километр Метр

• Миллиметр в милю (США)
• Миллиметр в морскую милю
• Миллиметр в ярд
• Морская миля в сантиметр
• Морская миля в фут

901 63 морская миля в дюйм

• морская миля в километр
• морская миля в метр
• морская миля в метр (США)
• морская миля в миллиметр
• морская миля в ярд
• ярд
• от
• ярд до
• Ярды в дюймы
• Ярды в километры
• Ярды в метры
• Ярды в мили (США)
• Ярды в миллиметры
• Ярды в морские мили

Метры в миллиметры Преобразование в миллиметры (метры в миллиметры)

Метры в миллиметры м в мм)

Введите метр (м) значение единицы длины в преобразовать метр в миллиметр .

Сколько миллиметров в метре?

В одном метре 1000 миллиметров.
1 метр равен 1000 миллиметру .
1 м = 1000 мм

Определение счетчика

метр — это единица СИ, принятая в науке как основная единица измерения расстояния и длины. Наряду с другими единицами измерения, такими как километр или дюйм, метр является одной из основных единиц в системе СИ. Один метр равен длине пути, который свет проходит в вакууме за время 1/299 792 458 секунд.Символ СИ для метра — м, а один метр равен 100 сантиметрам или 1/1000 ^-го (10 ^-3 ) километра.

Перевести метр

Миллиметровое разрешение

Миллиметр — одна из наиболее часто используемых единиц длины, равная 1/1000 ^или метра. Это единица СИ, используемая для измерения малых расстояний и малых длин. Согласно правилам СИ, условное обозначение единицы — мм .

Конвертировать Миллиметр

Преобразователь метрических единиц в миллиметры

Это очень простой в использовании преобразователь метра в миллиметр .Прежде всего, просто введите значение метров (м) в текстовое поле формы преобразования, чтобы начать преобразование метров в мм,
затем выберите десятичное значение и, наконец, нажмите кнопку преобразования, если автоматический расчет не сработал. Миллиметр Значение будет автоматически преобразовано при вводе.

Десятичное число — это количество цифр, которое необходимо вычислить или округлить в результате преобразования метра в миллиметр .

Вы также можете проверить таблицу преобразования метра в миллиметр ниже или вернуться к преобразователю метра в миллиметр вверх.

Примеры преобразования из метра в миллиметр

1 м = 1000 миллиметров

Пример для 2 метров:
2 Метр = 2 (Метр)
2 метра = 2 x (1000 миллиметров)
2 Метр = 2000 Миллиметров

Пример для 3 метра:
3 Метр = 3 (Метр)
3 метра = 3 x (1000 миллиметров)
3 Метр = 3000 Миллиметров

Пример для 15 метров:
15 Метр = 15 (Метр)
15 метров = 15 x (1000 миллиметров)
15 Метр = 15000 Миллиметров

 

Метр в Миллиметр Таблица преобразования

14

мм

мм

мм

901 41 37 м

9014 9014

9014

Измеритель	Миллиметр
1 м	1000 мм
2 м	2000 мм
3 м	3000 мм	9013
5 м	5000 мм
6 м	6000 мм
7 м	7000 мм
8 м	8000 мм
	9 м	9 м	10 м	10000 мм
11 м	11000 мм
12 м	12000 мм
13 м	13000 мм
142 142	15 м	15000 мм
16 м	16000 мм
17 м	17000 мм
18 м	18000 мм
19 м	19000 мм
20 м	20000 мм
21 м	21000 мм
22 м	22000 мм
24 м	24000 мм
25 м	25000 мм
26 м	26000 мм
27 м	2713000 мм
29 м	29000 мм
30 м	30000 мм
31 м	31000 мм
32 м	32000 мм
34 м	34000 мм
35 м	35000 мм
36 м	36000 мм
37000 мм
38 м	38000 мм
39 м	39000 мм
40 м	40000 мм
9014 9014 мм		42 м	42000 мм
43 м	43000 мм
44 м	44000 мм
45 м	45000 мм
		47 м	47000 мм
48 м	48000 мм
49 м	49000 мм
50 м	50000 мм

901

Измеритель	Миллиметр
50 м	50000 мм
55 м	55000 мм
60 м	60014 мм		652	60014 мм
70 м	70000 мм
75 м	75000 мм
80 м	80000 мм
85 м	85000 мм

9014 9014 9014

9014 95 м 95000 мм 100 м 100000 мм 105 м 105000 мм 110 м 110000 мм

9014 11514 9014

120 м 120000 мм 125 м 125000 мм 130 м 130000 мм

9013 2

135 м 135000 мм 140 м 140000 мм 145 м 145000 мм 150 м 150000 мм 4 160 м 160000 мм 165 м 165000 мм 170 м 170000 мм 175 м 175000 мм

9014 9014 180 м 185 м 185000 мм 190 м 1

мм

195 м 195000 мм 200 м 200000 мм

14 9014 205139 9014 9014 205 210 м 210000 мм 215 м 215000 мм 220 м 220000 мм

901 39 225 м 225000 мм 230 м 230000 мм 235 м 235000 мм 240 м 24000014 мм 240000 мм 250 м 250000 мм 255 м 255000 мм 260 м 260000 мм 265 м 26514000 мм 275 м 275000 мм 280 м 280000 мм 285 м 285000 мм 290 м

901 290 м

2

мм

901 2

мм 901

Общие значения из метра в миллиметр

• 1 м = 1000 мм
• 2 м = 2000 мм
• 3 м = 3000 мм
• 5 м = 5000 мм
• 10 м = 10000 мм
• 6 м = 6000 мм
• 12 м = 12000 мм
• 7 м = 7000 мм
• 0.5 м = 500 мм
• 4 м = 4000 мм
• 9 м = 9000 мм
• 50 м = 50000 мм
• 1000 м = 1000000 мм
• 1,5 м = 1500 мм
• 100 м = 100000 мм
• 0,000004 m = 0,004 мм
• 8 м = 8000 мм
• 8,8 м = 8800 мм
• 15 м = 15000 мм

Последние комментарии

© 2007-2021 www.conversion-metric.org

мм в дюймы + форма дроби

Определения

Содержание

Единица миллиметра

Миллиметр или миллиметр [мм] — это единица длины в системе единиц СИ.Он определяется как одна тысячная (1/1000) метра. Метр [м] — это основная единица длины в системе СИ, и в настоящее время он определяется как расстояние, проходимое светом в вакууме за frac {1} {299 , 792 , 458} секунд.

Общие кратные и дробные единицы счетчика определяются с помощью десятичных префиксов СИ, как показано в следующей таблице:

Единица	Символ	[м]
Нанометр	нм	10 -9
Микрометр	мкм	10 -6
Миллиметр	мм	0.001
Сантиметр	см	0,01
Гектометр	hm	100
Километр	км

Единица измерения в дюймах

Дюйм [дюйм] — это единица измерения длины в британской системе мер и системе единиц США. Исторически он задумывался как длина трех зерен ячменя.Сегодня это определяется с помощью метра в единицах СИ как: 1 дюйм = 0,0254 м (= 2,54 см = 25,4 мм).

Несколько единиц дюйма определены, как показано в таблице:

Единица	Символ	[дюйм]
Фут	фут	12

ярдов

36 Mile mi 63360

Как преобразовать дюймы в мм

• Умножьте расстояние в [дюймах] на 25.4
• Результат — расстояние в мм

Например, для преобразования 1/2 дюйма в мм выполните: 0,5 times 25,4 = 12,7 мм

Как преобразовать мм в дюймы

• Разделить расстояние в [мм ] на 25,4
• Результат — расстояние в дюймах

Например, чтобы преобразовать 150 мм в дюймы, выполните: 150 / 25,4 приблизительно 5,91 дюйма

Таблица преобразования из мм в дюймы

В В следующей таблице некоторые типичные расстояния в миллиметрах преобразованы в дюймы:

[мм]	[дюймы]
0.5	0,01969
1	0,03937
2	0,07874
3	0,1181
4 9014 9014 9014 9014

9014 9014 9014 0,4724 20 0,7874 30 1,181 40 1,575 50 1.969 100 3,937 200 7,874 300 11,81 400 15,714 400 15,714 700 27,56 800 31,5 900 35,43 1000 39.37

Таблица преобразования из дюймов в мм

В следующей таблице некоторые типичные расстояния в дюймах преобразованы в миллиметры:

[дюймы]	[мм]
0,125	3,175	3,175 90
0,25	6,35
0,375	9,525
0,5	12,7
1	25,4		28
3	76,2
5	127
10	254
12	304,8	4 9014 901 901	304,8

9014

50 1270

1000 мм в дюймы — преобразование 1000 мм в дюймы

Преобразование 1000 мм в дюймы, преобразование 1000 мм в дюймы, калькулятор 1000 мм в дюймы, преобразователь 1000 мм в дюймы, простой способ преобразования 1000 мм в дюймы, 1000 мм равно количеству дюймов, вы можете использовать наш калькулятор для быстрого преобразования 1000 мм в дюймы

Миллиметр — это единица измерения длины в системе СИ (метрическая система единиц СИ), определение миллиметра в Международной системе единиц (СИ), официально признанное Международным комитетом мер и весов, — (D1) ».Дюйм — это международная единица длины, равная ровно 25,4 миллиметра. Это единица длины в имперской системе мер,

.

США

Ответ: 1000 мм = 39,3701 дюйм

Формула в миллиметрах в дюймах:

Легко использовать и правильно писать метрические единицы, если вы знаете, как работает система. Он прост и логичен, состоит из единиц и префиксов.

Пример: вы хотите преобразовать 10 мм в дюймы

По формуле -> 10мм = 0.393701 дюймов

дюймов в миллиметр Формула:

1 дюйм (дюйм) = 25,4 миллиметра (мм)

Пример: вы хотите преобразовать 20 дюймов в миллиметры

По формуле ->

20 × 25,4 = 1000

Мм в дюймы (дюймы) Конвертер и расчеты:

Вы можете использовать наш конвертер для перевода 1000 мм в дюймы

Преобразование — это многоэтапный процесс, который включает в себя умножение или деление на числовой коэффициент, выбор правильного количества значащих цифр и округление.Следующие разделы предназначены в качестве руководства по этому многоэтапному процессу.

Преимущества нашего калькулятора:

На повседневную деятельность всегда прямо или косвенно влияли меры и преобразования:

1- Преобразование мм в дюймы

2- Легко и просто

3- Вы можете определить длину

4- Вы можете определить длину вручную

5- Проверьте длину самостоятельно дома

6- Рассчитать и узнать результат без калькулятора

Система

SI имеет множество преимуществ:

1- Только одна единица на каждое количество

2- Не нужно запоминать числа

3- Можно причудливо измерить любое физическое состояние

4- Имеет уникальные символы

Теперь вы можете получить ответ на все свои вопросы:

1- Преобразование 1000 мм в дюймы

2- Сколько дюймов в 1000 мм?

3- Как преобразовать 1000 мм в дюймы?

4- Сколько 1000 мм в дюймах

5-1000 мм преобразовано в дюймы

6-1000 мм преобразование в дюймы

7- Сколько 1000 мм в дюймах

8-1000 мм равно тому, сколько дюймов

9- Что такое 1000 мм в дюймах?

Конвертер из миллиметров в сантиметры ?

Используйте этот конвертер для простого преобразования из миллиметров в сантиметры (из миллиметров в сантиметры).

Быстрая навигация:

1. Сколько миллиметров в сантиметре?
2. Разница между миллиметрами и сантиметрами
3. Как преобразовать миллиметры в сантиметры
4. Таблица преобразования из миллиметров в сантиметры

Сколько миллиметров в сантиметре?

Миллиметры и Сантиметры — единицы измерения длины в метрической системе. Соответствующие сокращения: мм и см соответственно.

Эти две единицы являются производными от основной единицы СИ — метра. Приставка «милли» означает 1/1000, а «санти» — 1/100 доли. Следовательно, метр равен 1000 миллиметрам или 100 сантиметрам. Таким образом, если 1000 мм равняется 100 см, то 1 см равняется 10 мм .

Разница между миллиметрами и сантиметрами

Последнее официальное определение миллиметра связано с определением счетчика. В 1983 году было установлено, что основная единица равна длине пути, который свет проходит в вакууме за 1/299 792 458 секунд.0,001 метра в миллиметре означает, что миллиметр — это расстояние, которое свет проходит в вакууме за 1/299 792 458 000 секунд.

Обычно миллиметр — это единица измерения, используемая в технике и задачах, требующих высокой точности, поскольку он измеряет очень небольшие расстояния.

Как уже установлено, сантиметр равен 0,01 метра и равен 10 мм. Это устройство, которое позволяет точно и легко выполнять повседневные задачи. Например, портные используют сантиметры для принятия мер. Другое приложение — создание карт — реальные размеры адаптируются к масштабу карты с помощью сантиметров.Иногда количество осадков также измеряется в сантиметрах.

Как преобразовать миллиметры в сантиметры

Преобразование из миллиметров в сантиметры производится по следующей формуле:

мм / 10 = см .

Вы можете составить уравнение или просто переместить десятичную запятую на одну позицию влево.

Пример преобразования

мм в см

Пример задания: преобразовать 50 миллиметров в сантиметры .Решение:

Формула:
мм / 10 = см
Расчет:
50 мм / 10 = 5 см
Конечный результат:
50 мм равно 5 см

таблица преобразования из мм в см

таблица преобразования из мм в см

мм	см
1 мм	0,10 см
2 мм	0.20 см
3 мм	0,30 см
4 мм	0,40 см
5 мм	0,50 см
6 мм	0,60 см
7 мм	0,70 см
8 мм	0,80 см
9 мм	0,90 см
10 мм	1 см
20 мм	2 см
30 мм	3 см
40 мм	4 см
50 мм	5 см
60 мм	6 см
70 мм	7 см
80 мм	8 см
90 мм	9 см
100 мм	10 см
200 мм	20 см
300 мм	30 см
400 мм	40 см
500 мм	50 см
600 мм	60 см
700 мм	70 см
800 мм	80 см
900 мм	90 см
1000 мм	100 см

Список литературы

[1] Специальная публикация NIST 330 (2008) — «Международная система единиц (СИ)», под редакцией Барри Н.